Derrière ce mot barbare se cache vos pires souvenirs du collège. Oui je dis bien collège et non lycée, car dans mes souvenirs, il s'agit du programme de 4eme, honte à vous donc.
Commençons par ce petit dessin :
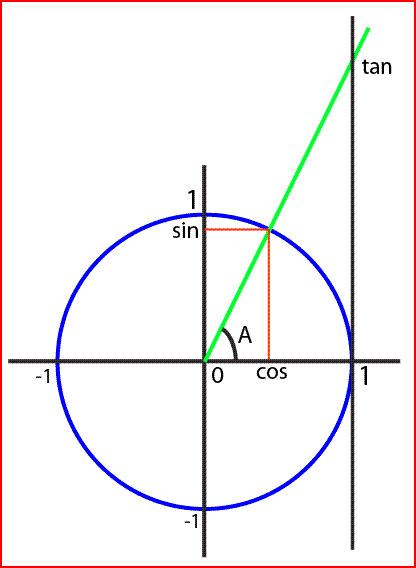
Petite précision avant tout. Le dessin ci dessus est celui que vous verrez partout.
Toutefois, le point [0,0] de la composition d'AE est en haut à gauche. Ca veut dire que Y augmente de valeur en descendant. Donc inversé le 1 et le -1 de l'axe verticale dans votre tete quand vous etes dans aE.
Alors alors, kénécé...
Nous allons voir la trigonométrie uniquement dans la partie qui nous interesse, celle qui s'applique à After Effect.
La trigonométrie nous dit ceci :
-A chaque angle correspond un sinus, un cosinus et une tangente.
-le cosinus et le sinus sont compris entre -1 et 1
-cos(A)+sin(A)=1
Comme vous le voyez sur le dessin, à l'angle A correspond un cosinus environ égale à 0,4, un sinus environ égale à 0,9, et une tangente environ égale à 2.
Pour le moment nous allons nous intéresser au cosinus et au sinus.
Le cercle ayant un rayon de 1, on comprend pourquoi sin et cos varient de -1 à 1. Et en faisant augmenter l'angle à vitesse constante, vous comprenez ainsi que le cos et le sin vont osciller de -1 à 1. vous comprenez également instinctivement que lorsque l'angle A est proche de 90° (barre verte verticale) le sin s'attarde autour de 1, puis replonge brusquement vers 0 puis -1.
C'est pour cela qu'on parle par exemple de courbe sinusoïdale. L'allé-retour est arrondi aux extrémité, il en va exactement de même pour le cosinus.
Grace à ce dessin, vous comprenez également que le sin et le cos soient des vases communicants.
Quand sin=1, alors cos=0, et inversement.
Mais alors concrètement, dans after effect, à quoi ça va nous servir ?
Très concrètement, à trois choses :
-traduire un angle en position.
-traduire une position en angle.
-créer un phénomène oscillatoire.
Comment ça traduire un angle en positon ???
Et bien oui, regarder le dessin. On comprend que pour l'angle A correspond un point sur le cercle, de coordonnées [cos,sin]
Et inversement, si on a un point de coordonnée [x,y], on peut donc trouver son angle par rapport à un autre objet.
Passons à un peu de pratique, et voyons un point important.
Vous ètes habitués aux angles en degrés, de 0 à 360. C'est d'ailleurs la mesure utilisée par AE pour les rotations.
MAIS pour la trigonométrie, on utilise non pas les degrés, mais les radians.
Alors avant de dire beurk, voyons ce que c'est.
Comme vous savez, le périmètre d'un cercle se trouve par cette "formule" : Pi*R*2, ou R est le rayon.
Ici, notre cercle a un rayon de 1, donc son périmètre vaut 2*Pi.
Voilà comment fonctionnent les radians.
L'angle A vaut la section du périmètre du cercle délimité par l'angle.
On comprend donc que si A=90 en degré, on a donc un 1/4 de cercle, l'angle A vaut donc Pi/2 en radian.
180 degré=Pi
270 degré=(3*pi)/2
etc
Mais ne vous inquiétez pas, vous n'aurez pas à les calculer, AE a une fonction qui sert à ça.
L'important est de le savoir pour ne pas faire d'erreur, c'est un grand classique.
Ca veut dire que quand on écrit cos(A), A doit etre en radian.
Et comme souvent, A sera en dégré (car récupéré sur la valeur de rotation d'un calque), on écrira ça :
cos ( degreesToRadians ( A ) )
Et quand on voudra faire l'inverse, on utilisera RadiansToDegrees, on verra dans quel cas.
Un peu de pratique pour détendre tout le monde.
Créez un petit calque carré.
Dans sa postion, écrivez ceci :
vitesse=2*Math.PI*time;
diametre=50;
x=Math.cos(vitesse)*diametre;
y=Math.sin(vitesse)*diametre;
[x,y]+value
Et hop, un petit carré qui tourne autour d'un centre, mais sans rotation, il s'agit de sa position. D'ailleurs comme le voyez, il reste droit comme un i.
Explication :
vitesse=2*Math.PI*time; on définit la variable, selon le temps ici. comme 2*Pi vaut un tour complet, on comprend quand quand time=1, ça fait 1 tour, quand time=3, ça fait 3 tours.
diametre=50; Comme cos et sin varient de -1 à 1, on comprend qu'il faille augmenter la valeur, sinon notre carré va tourner autour du cercle de base, qui va de -1 à 1, c'est tout petit.
x=Math.cos(vitesse)*diametre;
y=Math.sin(vitesse)*diametre;
[x,y]+value
La suite est sans histoire. J'ai rajouté +value, car sinon, le carré tournerait autour du coin supérieur gauche de votre composition, puisqu'il évoluerait dans les 2 dimensions de -50 à 50.
le +value permet donc de le placer où l'on veut, ou même de l'animer.
Et là vous vous dites "hey cool, je peux aussi changer au cours le diamètre pour créer une spirale !!"
oui oui, vous pouvez, faites donc.

