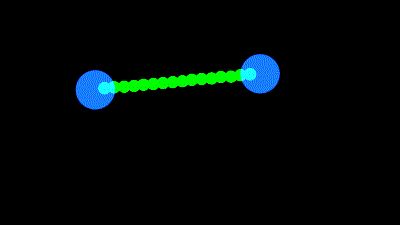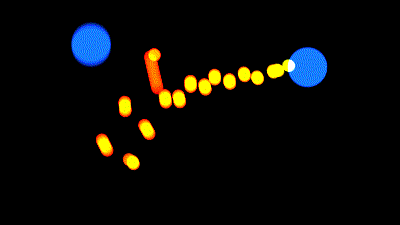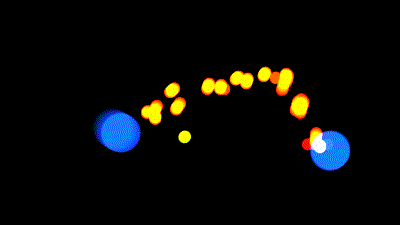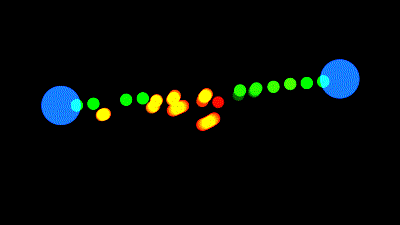
L'idée est la suivante :
Qu'importe la méthode pour bouger le carré, il se déforme tout seul quand il touche le sol.
Pour ça, nous allons non pas bouger le carré lui même, mais un Null.
Ensuite, on dira ceci au carré :
Tu suis le Null dans sa position, mais si ta position en Y atteint une certaine valeur, tu ne bouges sur Y.
On va déjà faire ça.
Créez un Null, et un petit carré. Rajoutez à ce petit carré un paramètre glissière, et nommez le "sol". Mettez y 350 (ma compo fait 480x360, je vous rappelle que 350, c'est en bas).
Dans le point d'ancrage du carré, corrigez Y pour qu'il soit en bas. Si votre carré fait 50x50, vous aurez donc [25,50].
Dans la position du carré, on va écrire ça :
N=thisComp.layer("Nul 1").transform.position; //position du Null
sol=effect("sol")("Curseur"); //valeur de "sol"
Y=Math.min(N[1],sol); // On dit que Y vaut la valeur minimum entre le y du Null, et la valeur de sol. Ainsi, quand le y du Null vaut plus que 350 (plus bas donc), Y garde la valeur du sol.
[N[0],Y] // On veut que le carré ait la valeur de x du Null pour x, et Y pour y.
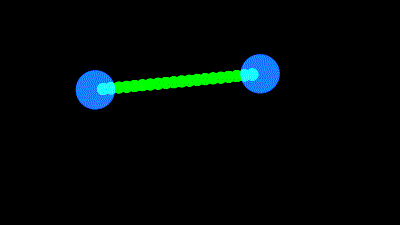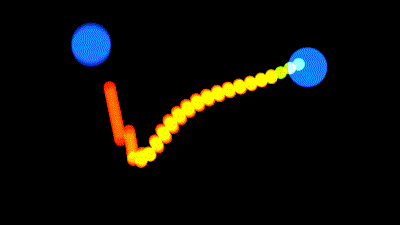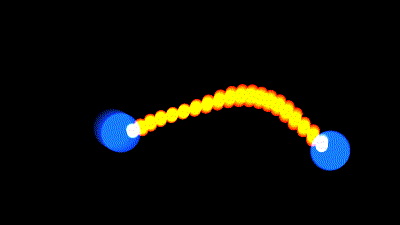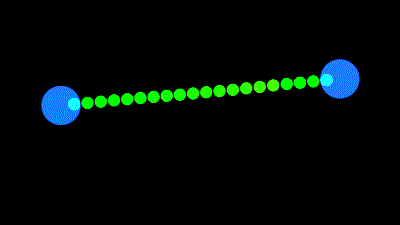
Bougez votre Null, le carré ne descendra pas sous la valeur du sol.
C'était quand même pas sorcier.
Passons à la déformation.
Voilà ce qu'on va dire au carré.
Plus tu es loin du Null, plus ton échelle sur X augmente, et plus ton échelle sur Y diminue.
Tout d'abord, rajoutez un paramètre glissière au carré, et nommez le "facteur", avec 3 comme valeur.
Écrivez dans l'échelle du carré :
p=position;
N=thisComp.layer("Nul 1").transform.position;
w=width;
F=effect("facteur")("Curseur");
Même pas mal.
Ensuite :
dist=p[1]-N[1];
Voilà, comme ça, on a une variable qui donne la distance verticale entre le carré et le Null. J'aurais même pu écrire dist=length(p,N), puisque de toute manière, ils ont toujours le même X.
Ca fonctionne car quand le carré est en l'air, dist vaut forcément 0 puisqu'il suit le Null. Mais quand il est au sol, c'est à ce moment que le Null se sépare du carré, et que dist prend une valeur non nulle.
x=linear(dist,-w/2,0,F*100,100);
y=linear(dist,-w/2,0,100/F,100);
Ca a l'air compliqué comme ça, mais en fait, non.
C'est simple, on veut ceci:
Plus le Null est loin, plus la déformation se fait.
Quand Null s'éloigne du carré, son Y est plus grand que celui du carré. Donc dist devient négatif.
C'est pour cela que j'ai choisi -w/2 comme distance de déformation : la moitié de la hauteur du carré. Ainsi, il suffit que le Null descende "d'un demi carré" pour que la déformation se fasse au maximum. C'est une valeur subjective, mais elle a le mérite d'être fonction de la taille du carré. On aurait pu aussi metre 2, 25 ou 250.
Et donc, quand dist=-w/2, et bien x=300, car nous avons mis 3 dans la valeur facteur.
Donc si on multiplie X par 3, on va diviser Y par 3.
D'où le 100/F, qui divise bien 100 par 3.
Et évidemment, la dernière ligne :
[x,y]
Et voilà, vous pouvez tester, ça fonctionne, plus le "facteur" est grand, plus la déformation sera grande (3 c'est déjà pas mal)
Vous remarquerez une finesse, le carré fait de légère rotation. Nous voulons évidemment que les rotations se fassent uniquement en l'air, et non quand le carré est au sol.
Pour la rotation :
haut=100;
bas=300;
F=ease(position[1],haut,bas,60,0);
wiggle(2,F)
En dessous de 300, la rotation vaut 0, et elle augmente quand y va de 300 jusqu à 100. Au delà de 100, elle se maintient.
Il ne reste plus qu'à bruiter tout ça, avec gout.
Pour que la hauteur du son varie, j'ai activé le remappage temporel pour chaque son, en mettant ça dans l'expression :
seedRandom(index,true);
max=thisComp.layer("Nul 1").effect("son max")("Curseur");
min=thisComp.layer("Nul 1").effect("son min")("Curseur");
R=random(min,max);
(time-inPoint)*R
max vaut 1.5 et min vaut 0.5
Ainsi, chaque son va à sa propre vitesse.
Pourquoi time-inPoint ?
time est fonction de la compo, pas de chaque calque.
Ainsi, si un calque commence à la seconde 5, à sa première image, time vaudra 5.
donc comme on veut partir de 0, on rajoute - inPoint (qui vaut la valeur du temps au début du calque)
C'est un moyen simple pour avoir la valeur de temps en partant de 0 au début du calque.
Petite astuce :
Sur ces deux animations, le mouvement du Null a été fait par dessin de trajectoire, et en m'appliquant à la souris pour faire un truc qui ressemble à quelque chose.
Toutefois, il n'est pas évident sur ce type de mouvement de s'arrêter en bas au bon endroit:
Si vous descendez trop, le carré va rester trop longtemps écrasé. Et si vous ne descendez pas assez, il ne vas pas être écrasé assez longtemps.
Voilà comment j'ai fait :
J'ai fait mon mouvement, ensuite j'ai sélectionné toutes les clefs de position crées, et je les ai déplacées pour que les clefs du bas soit au bon endroit.