Comme Chatton me tane, allons y...
En plus, c'était mon prochain article prévu donc bon...
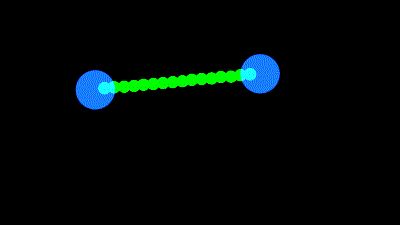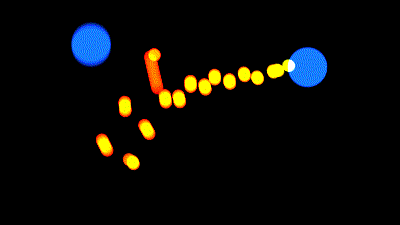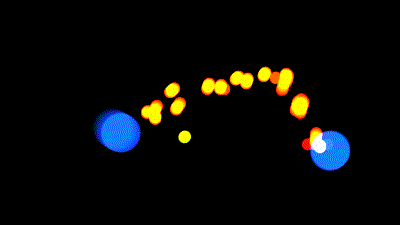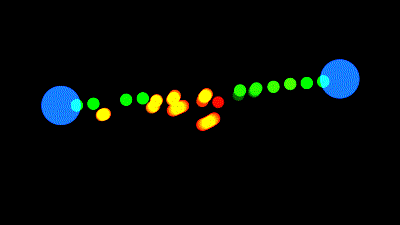
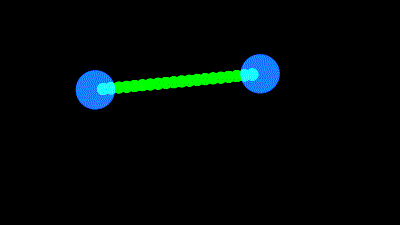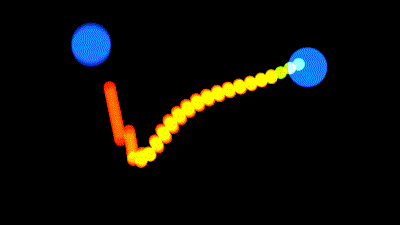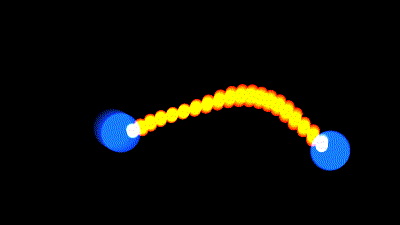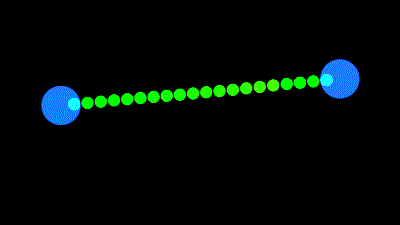
Je parle bien entendu de faire en sorte qu'un calque se déforme pour toujours avec la taille correspondant une distance donnée, comme dans l'exemple de fin de "look me in 2d"
Voilà comment faire, c'est vraiment tout bête:
Imaginons que nous avons une barre dont le point d'ancrage est à une extrémité.
Nous voulons que l'autre extrémité soit toujours "accrochée" à un autre calque (ou point de l'espace), que nous appellerons "target".
Voilà la démarche, on va prendre un exemple avec des chiffres, c'est plus simple à comprendre.
Imaginez que vous ayez un calque qui fasse 300 pixels de haut. Mais vous voulez qu'il ne fasse que 100. On comprend donc qu'il faut trouver le rapport entre ces 2 nombres.
Là c'est simple, le rapport est égal à 1/3, il faut que le calque soit à 33% (environ)
Il faut donc diviser la distance voulue par la hauteur du calque. Et oui, si le calque a la bonne taille à la base, on a bien 1/1=1.
Et comme c'est un pourcentage, il faut multiplier le tout par 100.
C'est donc super simple, ça donne ça :
poslook=comp("target Comp 1").layer("target").transform.position;
pos=transform.position;
dist=length(pos,poslook);
x=scale[0];
y=(dist/height)*100;
[x,y]
Ici on garde l'échelle sur X constante, et c'est Y qui va suivre la distance voulue.
Voilà, votre calque peut faire 10 et 1526 en hauteur, il sera toujours bien calé.
A vous de trouver comment ça peut vous servir !
Bonsoir à tous
jeudi 10 décembre 2009
mardi 17 novembre 2009
un peu de pub...
Allez, un peu de pub, une fois n'est pas coutume.
Guillaume Tel, série écrite et réalisée par votre serviteur, est enfin en ligne !
Le pilote (en bas) + les 3 premiers épisodes sont disponibles, puis ça sera un par semaine, pour un total de 17 épisodes.
GUILLAUME TEL
A bientot !
Guillaume Tel, série écrite et réalisée par votre serviteur, est enfin en ligne !
Le pilote (en bas) + les 3 premiers épisodes sont disponibles, puis ça sera un par semaine, pour un total de 17 épisodes.
GUILLAUME TEL
A bientot !
mercredi 16 septembre 2009
freezeur de composition
Un petit truc très rapide, qui peut servir à beaucoup de choses.
Vous avez besoin de bloquer une vidéo, ou une composition, sur une image donnée.
Comme vous le savez, vous pouvez faire clic droit sur un calque, "instant", "geler l'image".
Sauf qu'une fois que c'est fait, vous ne pouvez pas changer l'image en question. Pour ce faire, vous devez desactiver le remappage temporel, et refaire l'opération.
Voici une astuce pour choisir en un clin d'oeil l'image que vous voulez.
Créez un marqueur sur le calque. Pour se faire, vous pouvez appuyer sur la touche * avec le calque selectionné. Ensuite, clic droit dessus, paramètre, et nommez le 1 par exemple (autant avoir quelque chose de simple)
Ensuite, activez le remappage temporel du calque, et créez une expression dedans :
marker.key("1").time
On demande donc que le temps soit celui du marqueur qui s'appelle "1".
Et voilà ! L'image bloquée sera celle du marqueur. Déplacez le marqueur, et vous changerez l'image choisie.
Cela peut également servir pour une composition qui contient une image/photo différente à chaque frame.
A vous de voir à quel moment ça peut vous servir.
Vous avez besoin de bloquer une vidéo, ou une composition, sur une image donnée.
Comme vous le savez, vous pouvez faire clic droit sur un calque, "instant", "geler l'image".
Sauf qu'une fois que c'est fait, vous ne pouvez pas changer l'image en question. Pour ce faire, vous devez desactiver le remappage temporel, et refaire l'opération.
Voici une astuce pour choisir en un clin d'oeil l'image que vous voulez.
Créez un marqueur sur le calque. Pour se faire, vous pouvez appuyer sur la touche * avec le calque selectionné. Ensuite, clic droit dessus, paramètre, et nommez le 1 par exemple (autant avoir quelque chose de simple)
Ensuite, activez le remappage temporel du calque, et créez une expression dedans :
marker.key("1").time
On demande donc que le temps soit celui du marqueur qui s'appelle "1".
Et voilà ! L'image bloquée sera celle du marqueur. Déplacez le marqueur, et vous changerez l'image choisie.
Cela peut également servir pour une composition qui contient une image/photo différente à chaque frame.
A vous de voir à quel moment ça peut vous servir.
lundi 14 septembre 2009
le fil de téléphone
Bonjour à tous,
voici enfin l'explication de la dernière animation, le fil de téléphone.
Je vais aller relativement vite, car il n'y a ici rien de nouveau en terme d'outil.
Toute la difficulté est de découper le processus :
Nous voulons qu'un fil soit tendu par ses 2 extrémités, mais quand les extrémités sont trop proches l'une de l'autre, le fil se détend, et dessine une courbe vers le bas :

Créez votre petite scène : 2 ronds bleus (oui maintenant j'impose des contraintes), un petit rond blanc (au dessus des bleus), et un Null appelé "controle"
Pour le calque "controle", rajoutez 3 paramètre glissière, et nommez les "taille", "diametre" et "frequence". Merci.
"taille" va définir la taille du fil, c'est à dire la taille sous laquelle il commencera à fléchir, ça arrive aux meilleurs.
"diamètre" et "fréquence" nous serviront pour la spirale, pour la suite.
Créez également un Null "sol" à mettre sous le rond blanc. Vous connaissez le principe, on l'a déjà vu.
Ouvrez l'expression de position du rond blanc, et on y va :
plafond=thisComp.layer("controle");
I=index-plafond.index;
sol=thisComp.layer("sol");
nombre=sol.index-plafond.index-1;
Tout ça, c'est du déjà vu, j'explique pas.
Réfléchissons un peu. En gros, on veut que plus un rond est loin de chaque extrémité (donc au centre de la ligne), plus il va descendre selon la distance entre les 2 ronds bleus.
Il faut donc qu'on crée un valeur qui varie de 0 à 1. 0 correspond à un rond blanc à la même position qu'un rond bleu, et 1 au calque qui est pile poil au milieu.
pos=linear(I,1,nombre,0,1);
possin=ease(pos,0,1,0,Math.PI);
trigopos=Math.sin(possin);
pos vaut donc la position linéaire de chaque rond.
possin crée le sinus de pos. Visualisez le cercle trigo. Quand pos=0, possin=0, et quand pos=1, possin=Math.PI.
possin correspond donc à un arc de cercle allant de 0 à 180.
On comprend donc que trigopos vaut 1 quand possin vaut 0,5.
Rappelez vous de cette technique, c'est pratique pour crée un index en forme de bosse.
Pour possin, j'ai utiliser ease et non linear, ça évite que les premiers ronds blancs ne tombe tout de suite.
Bref, trigopos nous indique la distance des ronds blancs par rapport aux extrémités, en fonction de leur position dans la timeline (et non par rapport à leur distance réelle).
Créons ensuite les variables du calque "controle", ça sera fait :
taille=thisComp.layer("controle").effect("taille")("Curseur");
diametre=thisComp.layer("controle").effect("diamètre")("Curseur");
freq=thisComp.layer("controle").effect("freqence")("Curseur");
Commençons à placer les ronds. Je ne fais que reprender le même exercice qu'ici.
A=thisComp.layer("A").transform.position;
B=thisComp.layer("B").transform.position;
V=sub(B,A);
Les calques A et B sont évidemment mes ronds bleus.
ligne=A+V*pos;
On réutilise donc la position linéaire des calques pour les placer de la ligne.
Maintenant, occupons nous de la déformation :
dist=length(A,B);
Voilà, comme ça on a la distance entre les ronds bleus. Maintenant, nous devons la comparer à la "taille" :
delta=ease(dist,0,taille,Math.PI/2,0);
on a donc une valeur "delta" qui vaut 0 quand les ronds bleus sont aussi loin que "taille" (ou plus), et qui vaut Math.PI/2 quand les ronds bleus sont confondus.
G=(Math.sin(delta)*taille/2)*trigopos;
G est la valeur qui fait descendre nos ronds blancs :
Quand les ronds bleus sont confondus, on peut considérer que le fil est plié en 2, donc que le rond le plus bas sera descendu de taille/2 (c'est évidemment une approximation sans aucune prétention physique).
Quand delta=0, G=0 et n'est donc pas pris en compte.
Finalement, nous créons des potentiomètres, comme pour les lampes. On crée des variables qui vont de "éteind" à "allumé", et on se donne le droit d'utiliser les variables intermédiaire:
trigopos est l'interrupteur fonction de la position des ronds blancs.
delta est l'interrupteur fonction de la postion des ronds bleus.
courbe=ligne+ [0,G];
La déformation vaut donc la ligne, +G en Y.
Et voilà, vous avez votre fil qui se déforme. Vous pouvez multipliez votre ronds blancs, ça marche.
Passons à la spirale.
Alors alors, qu'est ce qu'on veut faire ici...
Nous voulons en fait créer une autre ligne, qui va suivre la 1ere, mais en forme de spirale.
C'est un peu comme si on collait un bout de plastique sur le rayon d'un vélo :
Quand le vélo avance, le bout de plastique suit la même trajectoire que le vélo, mais en suivant une spirale, ça s'appelle une cycloïde.
La différence, c'est qu'ici, ça n'est pas le mouvement qui fait faire des cercles au bout de plastique, mais la position des ronds, ce qui revient au même.
Vous pouvez vous entrainer en faisant ceci:
Créez un solide, utiliser cos en X et sin en Y, et faite varier l'angle avec son index.
Si vous dupliquez le solide, vous allez donc obtenir un cercle, nous avons déjà vu ça en long en large et en travers.
Mais si vous rajoutez une variable qui fait augmenter X en fonctione de l'index, vous aurez votre spirale.
C'est exactement ce que nous allons faire.
spiralX=Math.cos (pos*freq )*diametre;
spiralY=Math.sin (pos*freq )*diametre;
Simplissime, vous connaissez déjà tout ici.
Dernière ligne:
courbe+ [spiralX,spiralY]
Et voilà !
Vous remarquerez comme nous avons tout bien segmenté :
ligne+courbe+spirale.
C'est un bon moyen pour s'y retrouver et faire du travail propre.
J'avais dit que j'avais fait court, ça va quand même, c'est pas trop long.
Encore une fois, c'est évidemment du système D, mais ça fait la blague.
Par exemple, nous n'avons pas fait en sorte que la spirale suive le tracé, et aucun délai n'a été créé pour les ronds du milieu.
Mais si vous cherchez, je suis sur que vous trouverez...
voici enfin l'explication de la dernière animation, le fil de téléphone.
Je vais aller relativement vite, car il n'y a ici rien de nouveau en terme d'outil.
Toute la difficulté est de découper le processus :
Nous voulons qu'un fil soit tendu par ses 2 extrémités, mais quand les extrémités sont trop proches l'une de l'autre, le fil se détend, et dessine une courbe vers le bas :

Créez votre petite scène : 2 ronds bleus (oui maintenant j'impose des contraintes), un petit rond blanc (au dessus des bleus), et un Null appelé "controle"
Pour le calque "controle", rajoutez 3 paramètre glissière, et nommez les "taille", "diametre" et "frequence". Merci.
"taille" va définir la taille du fil, c'est à dire la taille sous laquelle il commencera à fléchir, ça arrive aux meilleurs.
"diamètre" et "fréquence" nous serviront pour la spirale, pour la suite.
Créez également un Null "sol" à mettre sous le rond blanc. Vous connaissez le principe, on l'a déjà vu.
Ouvrez l'expression de position du rond blanc, et on y va :
plafond=thisComp.layer("controle");
I=index-plafond.index;
sol=thisComp.layer("sol");
nombre=sol.index-plafond.index-1;
Tout ça, c'est du déjà vu, j'explique pas.
Réfléchissons un peu. En gros, on veut que plus un rond est loin de chaque extrémité (donc au centre de la ligne), plus il va descendre selon la distance entre les 2 ronds bleus.
Il faut donc qu'on crée un valeur qui varie de 0 à 1. 0 correspond à un rond blanc à la même position qu'un rond bleu, et 1 au calque qui est pile poil au milieu.
pos=linear(I,1,nombre,0,1);
possin=ease(pos,0,1,0,Math.PI);
trigopos=Math.sin(possin);
pos vaut donc la position linéaire de chaque rond.
possin crée le sinus de pos. Visualisez le cercle trigo. Quand pos=0, possin=0, et quand pos=1, possin=Math.PI.
possin correspond donc à un arc de cercle allant de 0 à 180.
On comprend donc que trigopos vaut 1 quand possin vaut 0,5.
Rappelez vous de cette technique, c'est pratique pour crée un index en forme de bosse.
Pour possin, j'ai utiliser ease et non linear, ça évite que les premiers ronds blancs ne tombe tout de suite.
Bref, trigopos nous indique la distance des ronds blancs par rapport aux extrémités, en fonction de leur position dans la timeline (et non par rapport à leur distance réelle).
Créons ensuite les variables du calque "controle", ça sera fait :
taille=thisComp.layer("controle").effect("taille")("Curseur");
diametre=thisComp.layer("controle").effect("diamètre")("Curseur");
freq=thisComp.layer("controle").effect("freqence")("Curseur");
Commençons à placer les ronds. Je ne fais que reprender le même exercice qu'ici.
A=thisComp.layer("A").transform.position;
B=thisComp.layer("B").transform.position;
V=sub(B,A);
Les calques A et B sont évidemment mes ronds bleus.
ligne=A+V*pos;
On réutilise donc la position linéaire des calques pour les placer de la ligne.
Maintenant, occupons nous de la déformation :
dist=length(A,B);
Voilà, comme ça on a la distance entre les ronds bleus. Maintenant, nous devons la comparer à la "taille" :
delta=ease(dist,0,taille,Math.PI/2,0);
on a donc une valeur "delta" qui vaut 0 quand les ronds bleus sont aussi loin que "taille" (ou plus), et qui vaut Math.PI/2 quand les ronds bleus sont confondus.
G=(Math.sin(delta)*taille/2)*trigopos;
G est la valeur qui fait descendre nos ronds blancs :
Quand les ronds bleus sont confondus, on peut considérer que le fil est plié en 2, donc que le rond le plus bas sera descendu de taille/2 (c'est évidemment une approximation sans aucune prétention physique).
Quand delta=0, G=0 et n'est donc pas pris en compte.
Finalement, nous créons des potentiomètres, comme pour les lampes. On crée des variables qui vont de "éteind" à "allumé", et on se donne le droit d'utiliser les variables intermédiaire:
trigopos est l'interrupteur fonction de la position des ronds blancs.
delta est l'interrupteur fonction de la postion des ronds bleus.
courbe=ligne+ [0,G];
La déformation vaut donc la ligne, +G en Y.
Et voilà, vous avez votre fil qui se déforme. Vous pouvez multipliez votre ronds blancs, ça marche.
Passons à la spirale.
Alors alors, qu'est ce qu'on veut faire ici...
Nous voulons en fait créer une autre ligne, qui va suivre la 1ere, mais en forme de spirale.
C'est un peu comme si on collait un bout de plastique sur le rayon d'un vélo :
Quand le vélo avance, le bout de plastique suit la même trajectoire que le vélo, mais en suivant une spirale, ça s'appelle une cycloïde.
La différence, c'est qu'ici, ça n'est pas le mouvement qui fait faire des cercles au bout de plastique, mais la position des ronds, ce qui revient au même.
Vous pouvez vous entrainer en faisant ceci:
Créez un solide, utiliser cos en X et sin en Y, et faite varier l'angle avec son index.
Si vous dupliquez le solide, vous allez donc obtenir un cercle, nous avons déjà vu ça en long en large et en travers.
Mais si vous rajoutez une variable qui fait augmenter X en fonctione de l'index, vous aurez votre spirale.
C'est exactement ce que nous allons faire.
spiralX=Math.cos (pos*freq )*diametre;
spiralY=Math.sin (pos*freq )*diametre;
Simplissime, vous connaissez déjà tout ici.
Dernière ligne:
courbe+ [spiralX,spiralY]
Et voilà !
Vous remarquerez comme nous avons tout bien segmenté :
ligne+courbe+spirale.
C'est un bon moyen pour s'y retrouver et faire du travail propre.
J'avais dit que j'avais fait court, ça va quand même, c'est pas trop long.
Encore une fois, c'est évidemment du système D, mais ça fait la blague.
Par exemple, nous n'avons pas fait en sorte que la spirale suive le tracé, et aucun délai n'a été créé pour les ronds du milieu.
Mais si vous cherchez, je suis sur que vous trouverez...
dimanche 30 août 2009
telephone
Après le SOS de Fred, j'ai trouvé la problématique intéressante, et relativement concrète.
Voici donc ma solution :

Je posterai la solution surement la semaine prochaine, parce que là, pas trop le temps (et oui, l'expression n'est pas très compliquée (environ 35 lignes, ya pire), mais écrire l'article, c'est un peu plus long...)
Voici donc ma solution :

Je posterai la solution surement la semaine prochaine, parce que là, pas trop le temps (et oui, l'expression n'est pas très compliquée (environ 35 lignes, ya pire), mais écrire l'article, c'est un peu plus long...)
samedi 25 juillet 2009
Molécule
Bonjour bonjour,
de retour parmi vous, nous allons utiliser un peu de trigo pour faire ça :
La question est évidemment de trouver comment bien placer la balle rouge.
Une 1ere solution pourrait biensur être de déplacer le point d'ancrage de la balle rouge, pour que la rotation se fasse autour de la balle jaune.
Toutefois, ça n'est pas terrible, car cela utiliserait la rotation, alors que la position deviendrait inutilisable.
Nous allons donc utiliser la position pour faire tourner la balle rouge autour de la jaune.
Rappelez vous, la trigo nous permet de tranformer une rotation en position.
Créez vos 2 baballes, puis ajoutez deux paramètres glissières à la balle rouge en les nommant "distance" et "angle".
Dans la position de la balle rouge, commençons par :
distance=effect("distance")("Curseur");
angle=degreesToRadians ( effect("angle")("Curseur"));
target=thisComp.layer("Orange uni 1");
target sera donc notre balle jaune.
Je n'explique pas hein. La suite :
P=target.position;
Voilà, P sera le centre de rotation.Maintenant on cherche la distance entre la boule jaune et la boule rouge.
Cette distance est égale à la moitié du diamètre de la boule jaune + la moitié du diamètre de la boule rouge.
D=(target.width*target.scale[0]/100)/2 + (width*scale[0]/100)/2 +distance;
Ca parait confus, mais les parties rouges font en sorte que le changement d'échelle soit pris en compte.
Le +distance fait donc référence au paramètre glissière, et permet donc à la balle rouge de se décoller de la balle jaune, quand la valeur de distance vaut plus de 0.
La suite :
x=Math.cos (angle)*D;
y=Math.sin(angle)*D;
P+[x,y]
Pour mon animation, j'ai créé une expression wiggle dans l'angle, mais on fait évidemment ce qu'on veut.
Tout ça vous connaissez. A la fin, on rajoute P à x et y pour que P soit tjs le centre.
Dans l'animation, j'ai donc placé un wiggle dans l'échelle de la balle jaune :
x=wiggle(1,100);
[x[0] , x[0] ]
Pourquoi n'ai je pas juste écrit :
wiggle(1,100)
Testez, et vous verrez qu' After Effect vous créera un wiggle différent pour chaque dimension.
Et oui, n'oubliez pas, le wiggle est un mot particulier, qui crée un nombre de variables égale au nombre de valeur présente : 1 pour la rotation, 2 pour l'échelle, 3 pour une position 3d...
Maintenant, utilisons la rotation pour faire roule la balle sur l'autre:

Ouvrez la rotation de la balle rouge :
target=thisComp.layer("Orange uni 2");
angle=effect("angle")("Curseur");
Ca, vous connaissez. La différence avec la position, c'est qu'ici, l'angle est égale à la valeur du paramètre glissière, et non à sa valeur degreesToRadians. En effet, pour la position, on avait besoin de la valeur en radians, car cette dernière était contenu dans un Math.cos et Math.sin.
Plus la balle rouge est petite, plus elle va tourner vite. Il faut donc créer une variable qui définit la différence de périmètre entre la balle jaune et la balle rouge :
p=width*(scale[0]/100)*Math.PI;
P=target.width*(target.scale[0]/100)*Math.PI;
ratio=P/p;
On applique tout simplement la formule "diamètre * pi". Sauf que comme les deux ont *PI, on peut le retirer :
p=width*(scale[0]/100);
P=target.width*(target.scale[0]/100);
ratio=P/p;
Ensuite, il faut savoir que pour qu'une balle fasse un tour autour d une balle d un même diamètre, elle fait 2 tours. Testez, vous verrez.
On a donc pour la dernière ligne :
angle*2*ratio
Et voilà !
de retour parmi vous, nous allons utiliser un peu de trigo pour faire ça :
La question est évidemment de trouver comment bien placer la balle rouge.
Une 1ere solution pourrait biensur être de déplacer le point d'ancrage de la balle rouge, pour que la rotation se fasse autour de la balle jaune.
Toutefois, ça n'est pas terrible, car cela utiliserait la rotation, alors que la position deviendrait inutilisable.
Nous allons donc utiliser la position pour faire tourner la balle rouge autour de la jaune.
Rappelez vous, la trigo nous permet de tranformer une rotation en position.
Créez vos 2 baballes, puis ajoutez deux paramètres glissières à la balle rouge en les nommant "distance" et "angle".
Dans la position de la balle rouge, commençons par :
distance=effect("distance")("Curseur");
angle=degreesToRadians ( effect("angle")("Curseur"));
target=thisComp.layer("Orange uni 1");
target sera donc notre balle jaune.
Je n'explique pas hein. La suite :
P=target.position;
Voilà, P sera le centre de rotation.Maintenant on cherche la distance entre la boule jaune et la boule rouge.
Cette distance est égale à la moitié du diamètre de la boule jaune + la moitié du diamètre de la boule rouge.
D=(target.width*target.scale[0]/100)/2 + (width*scale[0]/100)/2 +distance;
Ca parait confus, mais les parties rouges font en sorte que le changement d'échelle soit pris en compte.
Le +distance fait donc référence au paramètre glissière, et permet donc à la balle rouge de se décoller de la balle jaune, quand la valeur de distance vaut plus de 0.
La suite :
x=Math.cos (angle)*D;
y=Math.sin(angle)*D;
P+[x,y]
Pour mon animation, j'ai créé une expression wiggle dans l'angle, mais on fait évidemment ce qu'on veut.
Tout ça vous connaissez. A la fin, on rajoute P à x et y pour que P soit tjs le centre.
Dans l'animation, j'ai donc placé un wiggle dans l'échelle de la balle jaune :
x=wiggle(1,100);
[x[0] , x[0] ]
Pourquoi n'ai je pas juste écrit :
wiggle(1,100)
Testez, et vous verrez qu' After Effect vous créera un wiggle différent pour chaque dimension.
Et oui, n'oubliez pas, le wiggle est un mot particulier, qui crée un nombre de variables égale au nombre de valeur présente : 1 pour la rotation, 2 pour l'échelle, 3 pour une position 3d...
Maintenant, utilisons la rotation pour faire roule la balle sur l'autre:

Ouvrez la rotation de la balle rouge :
target=thisComp.layer("Orange uni 2");
angle=effect("angle")("Curseur");
Ca, vous connaissez. La différence avec la position, c'est qu'ici, l'angle est égale à la valeur du paramètre glissière, et non à sa valeur degreesToRadians. En effet, pour la position, on avait besoin de la valeur en radians, car cette dernière était contenu dans un Math.cos et Math.sin.
Plus la balle rouge est petite, plus elle va tourner vite. Il faut donc créer une variable qui définit la différence de périmètre entre la balle jaune et la balle rouge :
p=width*(scale[0]/100)*Math.PI;
P=target.width*(target.scale[0]/100)*Math.PI;
ratio=P/p;
On applique tout simplement la formule "diamètre * pi". Sauf que comme les deux ont *PI, on peut le retirer :
p=width*(scale[0]/100);
P=target.width*(target.scale[0]/100);
ratio=P/p;
Ensuite, il faut savoir que pour qu'une balle fasse un tour autour d une balle d un même diamètre, elle fait 2 tours. Testez, vous verrez.
On a donc pour la dernière ligne :
angle*2*ratio
Et voilà !
samedi 18 juillet 2009
vendredi 22 mai 2009
et bah alors ?
Et oui, beaucoup de travail en ce moment, je reviens bientôt avec de nouvelles choses, promis.
En attendant, vous avez à faire !
En attendant, vous avez à faire !
lundi 27 avril 2009
mise à jour
Vous remarquerez que je suis en train de mettre tous les posts à jour, en commençant par les plus récents.
En effet, ce blog est construit de telle sorte que s'il y a une fonction qui vous échappe, vous en trouverez obligatoirement son explication dans un post précédent.
Donc à présent, toutes les expressions sont en rouge, sauf les mots clefs qui ont une explication entière dans un post. Ces derniers sont en bleu, et sont des liens vous emmenant au post correspondant !
vous pourrez ainsi cliquer sur le mot inconnu (en cliquant sur votre molette pour avec un nouvel onglet) pour avoir son explication, et garder un œil sur l'expression du jour.
En effet, ce blog est construit de telle sorte que s'il y a une fonction qui vous échappe, vous en trouverez obligatoirement son explication dans un post précédent.
Donc à présent, toutes les expressions sont en rouge, sauf les mots clefs qui ont une explication entière dans un post. Ces derniers sont en bleu, et sont des liens vous emmenant au post correspondant !
vous pourrez ainsi cliquer sur le mot inconnu (en cliquant sur votre molette pour avec un nouvel onglet) pour avoir son explication, et garder un œil sur l'expression du jour.
mercredi 22 avril 2009
je t'aime, moi non plus.

Aujourd'hui, quelque chose de rapide et simple.
Utilisons les vecteurs autrement. Nous allons faire en sorte que des objets soient attirés ou repoussés pas un autre.
Ne vous attendez pas à une entière simulation du champs électromagnétique, il s'agit juste d'une petite astuce.
Créez un Null "controle", et rajoutez lui 4 paramètres glissière : min, max, force et chaos.
Créez un solide, puis un autre, plus petit, et ouvrez la position de ce dernier.
C'est parti.
min=thisComp.layer("controle").effect("min")("Curseur");
max=thisComp.layer("controle").effect("max")("Curseur");
force=thisComp.layer("controle").effect("force")"Curseur")/100;
chaos=thisComp.layer("controle").effect("chaos")("Curseur");
J'ai divisé force par 100, car ça sera un réglage fin.
seedRandom(5,true);
hasard=random(-chaos,chaos);
Ça, ça sera donc pour la partie hasard si on en veut.
target=thisComp.layer("target").transform.position;
P=position;
vecteur=sub(P,target);
distance=length(vecteur);
F=ease(distance,min,max,force+chaos,0);
P+vecteur*F
Voilà, vous connaissez déjà tous les outils. On crée le vecteur qui va de la cible au calque, et on fait en sorte que plus la cible est proche, plus on "rajoute du vecteur" à la position du calque.
Comme on multiplie le vecteur par F, qui est au final la valeur de la force, vous comprenez pourquoi "force" doit rester petit.
Petite astuce, si vous rajouter à peu près la même expression dans l'échelle, en faisant en sorte, avec un truc du genre:
ease(distance,min,max,150,100);
Les calque grossiront quand ils seront proches de la cible. On aura ainsi l'impression qu'ils passent au dessus du calque cible.
Si vous mettez une valeur de force négative, les calques seront attirés par la cible.
Seul bémol de ce système D, le déplacement se fait par rapport à la position du calque AVANT l'expression. Donc si la cible passe très proche du calque dans sa position originale, le calque passera proche de la cible.
Mais bon, hein....
Il y a plein d'utilisation de cette expression, on peut aussi animer les valeurs max et force.

dimanche 19 avril 2009
marchons carré

L'astuce du jour à plusieurs mérites :
-La technique est relativement simple, vous en connaissez tous les outils (si vous avez tout lu!), la difficulté se trouve plutôt dans la traduction de ce que l'on veut produire dans After Effect.
-Cette animation est infaisable avec des clefs.
Je parle de mérite, car ce sont les deux points principaux que j'essaye de développer sur ce blog.
Aujourd'hui, nous allons faire marcher un carré !
Alors alors....Analysons ce que nous voulons dire à After Effect.
Nous allons devoir créer une expression pour la position. Le mouvement sur X est simple, et celui sur Y sautille. Nous devons également créer une expression pour la rotation, et que tout ce beau monde soit synchrone.
C'est parti.
Créez un solide carré, la taille vous regarde.
Rajoutez lui un paramètre glissière, et nommez ce dernier "vitesse". Mettez 300 dans ce paramètre glissière comme valeur de base.
Commençons par la position. Pour le moment, on ne vas s'occuper que de X.
temps=time-inPoint;
V=effect("vitesse")("Curseur");
x=temps*V;
y=value[1];
[x,y]+value
Rien de bien méchant, on demande à ce que le carré se déplace de 300 pixels/sec vers la droite.
On fera Y après. Comme on l'a déjà vu, temps=time-inPoint permet d'avoir une variable de temps qui comme à 0 au moment où le calque commence.
Passons à la rotation.
Commençons par comprendre ce dont on a besoin.
Plus le carré est grand, moins il doit faire de rotation pour une même distance.
En fait, à chaque fois qu'il parcoure une distance égale à la longueur de son coté, il fait une rotation de 90° :
temps=time-inPoint;
V=effect("vitesse")("Curseur");
cote=width*scale[0]/100;
x=temps*V;
Rien de bien méchant, on retrouve ainsi la valeur de X, qui nous donne la distance parcourue par le carré.
On a également créer "cote". Il vaut la largeur multipliée par l'échelle, divisé par 100. Ainsi, on pourra modifier la taille du carré directement par l'échelle sans passer par les propriétés du calque. Je divise par 100 puisque l'échelle 1 vaut 100.
Donc on a dit que pour chaque "cote" parcouru, le carré tourne de 90°. on a donc :
(x/cote)*90
Et voilà, on a écrit notre rotation. Il y a plein de façon de trouver la même valeur, c'en était une.
Passons à Y.
Si on regarde notre animation, on comprend qu'à chaque fois que notre carré est à 45°, il doit être au plus haut, en tenant donc sur son coin du bas. Il faut donc trouver de combien.
Comme vous le savez, a²+b²=c² quand abc est un triangle rectangle donc C est l'hypothénuse.
Ici, nous avons un carré, donc a=b. Donc imaginons que a=1, on a donc c=racine carrée de 2.
Cette valeur est très connue, mais un petit rappel de raisonnement ne fait pas de mal.
Le point de rotation est bien évidemment au centre. De combien monte-il ?
Voilà un petit dessin (fait exprès pour vous !) avec lequel c'est tout simple:
Assis, notre carré mesure X. Debout, il mesure donc XX=X multiplié par racine carré de 2.
La différence est donc XX-X. Cette différence est valable pour le point le plus haut du carré selon sa position, mais pour le centre du carré, il s'agit donc de la moitie.
On a donc :
V=effect("vitesse")("Curseur");
cote=width*scale[0]/100;
diagonale=cote*Math.pow(2,.5);
montee=(diagonale-cote)/2;
Voilà, on sait de combien doit monter le carré : "montee"
Maintenant, il faut qu'on trouve à quel moment.
Comme on l'a dit, il faut qu'il soit au plus haut quand le carré est à 45°.
C'est le moment de se remettre en tête le cercle trigo.
Nous allons utiliser le sinus. Le sinus vaut sa plus haute valeur, 1, quand l'angle est à 90°. Pour toujours avoir une valeur positive (puisque le carré doit "rebondir" et non avoir un mouvement sinusoïdale), nous allons utiliser Math.abs.
Le sinus vaut 1 tous les 180°. Or, nous avons besoin que le sin valle 1 tous les 90°. Il faut donc que la fréquence de la rotation soit doublée pour avoir un sin=1 tous les 90°.
Ce qui est chouette, c'est qu'on est en train de faire une pierre deux coups:
En effet, on a besoin que sin=1 quand rotation=45. Or, sin=1 quand rotation=90. Il faudrait décaler la valeur de 45 pour corriger ça, sauf que ça n'est pas la peine:
Etant donné qu'on a multiplié l'angle par 2, quand la rotation vaut 45, sa valeur dans l'expression vaudra donc 90 ! Donc tout rentre dans l'ordre.
Ouf, vous pouvez lacher votre apnée, voilà les dernières lignes:
y=Math.abs ( Math.sin ( degreesToRadians ( (rotation))*2))*-montee;
Regardez bien, il y a un - devant montee. Ca permet d'avoir la valeur négative de la variable sans devoir écrire montee*-1. Pourquoi *-1 d'ailleurs ? Car dans After Effect, le 0 de Y est en haut, donc si on veut qu'un calque monte, il faut que Y baisse.
La dernière ligne :
[x,y]+value
Le +value permet biensur de pouvoir mettre votre carré où vous voulez pour le départ.
Et voilà ! Vous avez un carré qui marche !
Vous pouvez biensur mettre une valeur négative dans la vitesse pour aller de droite à gauche.
vous pouvez modifier l'échelle. Si vous faites un carré plus grand, il tournera moins vite, et inversement avec un carré plus petit.
Installez 3 carrés de 3 tailles différentes, avec la meme vitesse. Vous verrez que les 3 iront à la même vitesse, meme si le plus petit a l'air de franchement galérer pour suivre les deux autres.
Ce que vous ne pouvez pas faire :
Changer la taille du carré dans le temps. En effet, sans rentrer dans les détails, dans cette expression, on ne rajoute pas à chaque image une valeur de position et de rotation. Pour chaque image, After Effect calcule l'image comme unique. Si vous changez l'échelle dans le temps, il va replacer le carré à chaque image comme si sa taille avait toujours été celle de l'image courante.
Vous pouvez également enlever les "time", et ainsi faire bouger votre carré en animant la valeur "vitesse"

vendredi 17 avril 2009
un exercice pour ce week end
ça vous rappelle rien ?... Les indices du jour sont :
-particular (Tracpode), j'ai pas testé avec Particle Word ou autre...
-l'expression magique est utilisée en partie à 2 endroits.
Aller hop ! au boulot. Vous avez droit à une question sous forme de commentaire.
-particular (Tracpode), j'ai pas testé avec Particle Word ou autre...
-l'expression magique est utilisée en partie à 2 endroits.
Aller hop ! au boulot. Vous avez droit à une question sous forme de commentaire.
jeudi 16 avril 2009
amélioration des lumières
Nous allons aujourd'hui essayer d'améliorer le système d'éclairage d'After Effect.
Comme vous le savez, After Effect propose plusieurs type d'éclairage, point, concentré, parallèle, ambiante.
Nous allons nous interesser aux plus utilisés, point et concentré (le spot).
After Effect permet de gérer en gros les ombres, les ombres douces, le spéculaire, la puissance. Il gère également l'angle camera-objet-lumière.
Il y a un paramètre que After Effect ne gère pas, c'est la déperdition de la puissance lumineuse. En effet, qu'importe la distance objet-lampe, l'objet reste toujours autant éclairé. Hors, bien évidemment, plus la lampe est loin de l'objet, moins la puissance est grande.
On va corriger ça, autant que faire ce peut.
Voilà notre schéma du jour:
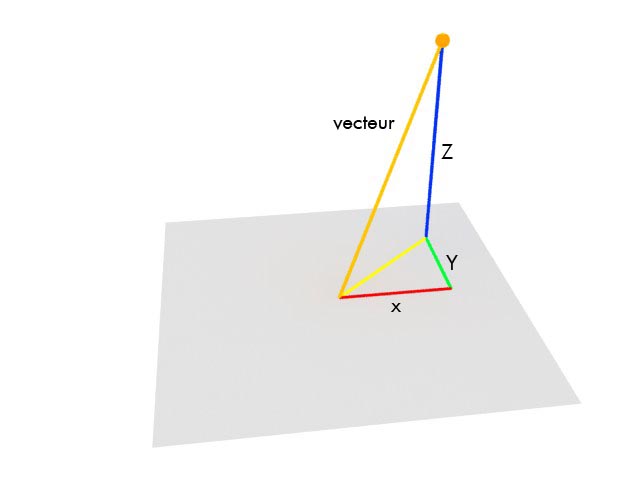
La boule jaune, c'est la lumière, et en bas, c'est le calque.
Alors on pourrait se dire :
"Et bah on assimiler la distance lampe-calque à la "diffuse" du calque !"
C'est en effet ce que l'on va faire, mais il y a un léger hic. AE éclaire le calque de manière uniforme (sans prendre en compte le spéculaire). Imaginez que la lampe se déplace sur le plan parallele au calque (donc là sur l'axe XY), la distance lampe-calque va augmenter.
Hors, si le calque fait 2000x2000, et que la le calque se déplace de 1000 sur X, la lumière va baisser (car la distance augmente), alors que la lumière est toujours "au dessus" du calque.
Nous allons donc séparer la distance Z, et la distance XY (la ligne jaune au sol)
Aller c'est parti.
Créons un calque Null de control, qui va nous permettre de regler l'atténuation. Ajoutez 2 paramètre glissère, "début" et "fin"
Créez également une lumière "point".
Créez un 1er calque 3d, aller dans le paramètre diffuse, et écrivez :
a=position; b=thisComp.layer("Lumière 1").transform.position;
debut=thisComp.layer("controle lumiere").effect("debut")("Curseur");
fin=thisComp.layer("controle lumiere").effect("fin")("Curseur");
J'explique pas.
La suite:
V=sub(b,a);
Vec=fromWorldVec(V);
La 1ere ligne, vous connaissez, on crée un vecteur de a vers b.
Pour la 2eme, je m'explique.
Voyez sur le dessin la ligne orange, le vecteur. C'est un vecteur qui appartient à l'espace général de AE. Nous avons besoin que ce vecteur soit regardé par le calque, pour pouvoir séparer Z,X et Y. C'est le role de fromWorldVec. On change de référenciel, du "monde" vers le calque.
On se libère ainsi des valeurs de rotation du calque.
distanceZ=Math.abs(Vec[2]);
On récupère ainsi la composante Z du vecteur. Si on avait faire ça avec V et non Vec, la composante Z ([2]) aurait été celle du monde AE, qu'importe l'angle du calque.
Le math.abs permet d'éviter le probleme d'orientation du calque.
Voilà, on a crée une valeur qui donne la distance perpendiculaire du calque vers la lampe.
valz=ease(distanceZ,debut,fin,value,0);
Là on a crée la valeur de la diffuse en fonction de distanceZ.
Vous comprenez ainsi que la valeur "début" doit correspondre au début de l'atténuation, et "fin" doit correspondre à la distance où le calque sera noir.
Passons à l'atténuation sur le plan parallèle au calque, le plan XY.
On va faire en sorte que la déperdition commence à début+"en gros la taille du calque". Ainsi, si début=0, l'atténuation commencera quand la lampe "sortira" du calque.
distanceM=(width+height)/4;
distanceXY=Math.abs ( add(Vec[0],Vec[1]) );
valXY=ease(distanceXY,debut+distanceM,fin+distanceM,value,0);
On crée donc une variable très approximative (mais ça fonctionne pas trop mal).
C'est donc la moyenne entre la largeur et la hauteur du calque (width+height)/2, que je redivise par 2, pour n'avoir que la moitié. En effet, on considèrera que le point d'ancrage est au milieu du calque.
Ensuite, on crée la longueur du trait jaune (sur le dessin), c'est à dire la projection du vecteur sur le calque. "add" fait l'addition de 2 vecteurs. Regardez le dessin, on voit bien que x+y=trait jaune.
Ensuite, on fait la même chose que pour Z, mais avec XY. C'est pour cela qu'on rajoute distanceM à début et fin, pour tout décaler.
La dernière ligne :
Math.pow(valz*valXY,.5);
C'est donc la multiplication des 2 valeurs crées, le tout à la racine carrée.
Ainsi, on reste au maximum à 50, et quand une des 2 valeurs est à 0, le tout est bien à 0.
On peut évidemment remplacer les 0 par une valeur positive, pour ne jamais avoir de calque noir.
Voilà, ça aide un peu, ça a ses limites... Si vous voulez utiliser une valeur spéculaire pour le calque, copier l'expression également dedans.
Aller, l'expression en entier :
a=position; b=thisComp.layer("Lumière 1").transform.position;
debut=thisComp.layer("controle lumiere").effect("debut")("Curseur");
fin=thisComp.layer("controle lumiere").effect("fin")("Curseur");
V=sub(b,a);
Vec=fromWorldVec(V);
distanceZ=Math.abs(Vec[2]);
valz=ease(distanceZ,debut,fin,value,0);
distanceM=(width+height)/4;
distanceXY=Math.abs ( add(Vec[0],Vec[1]) );
valXY=ease(distanceXY,debut+distanceM,fin+distanceM,value,0);
valeur=Math.pow(valz*valXY,.5);
Ca marche avec une seule lampe, c'est compliqué de le faire avec plusieurs lampes pour plusieurs raison :
On utilise un gros système D, qui fait que le calque devient lui meme plus sombre selon la distance de la lampe. Donc s'il y a une lampe rouge et une lampe bleue, et que la lampe bleu est loin, et la lampe rouge, ça ne marche pas : le calque sera bien éclairé car la rouge est proche, mais le calque sera donc violet, à cause de la lumière bleue.
Voilà, j'espère avoir été clair !
Plus début et fin sont petits, plus l effet sera fort.
Rechargez la page pour que les 2 animations soient syncrho.
avec:

sans:
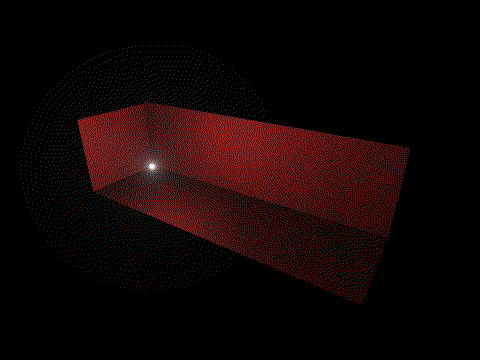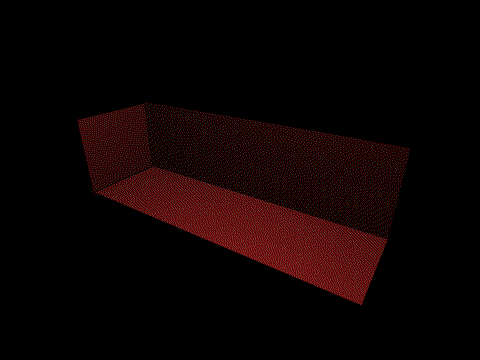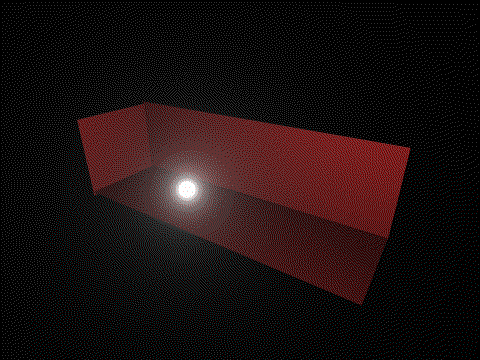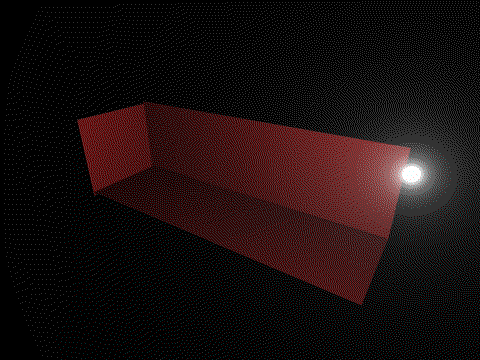
un autre exemple, notez dans le "avec" le coin supérieur gauche qui s'assombri, et évidemment, tout devient noir quand la lumière monte trop haut.
Comme vous le savez, After Effect propose plusieurs type d'éclairage, point, concentré, parallèle, ambiante.
Nous allons nous interesser aux plus utilisés, point et concentré (le spot).
After Effect permet de gérer en gros les ombres, les ombres douces, le spéculaire, la puissance. Il gère également l'angle camera-objet-lumière.
Il y a un paramètre que After Effect ne gère pas, c'est la déperdition de la puissance lumineuse. En effet, qu'importe la distance objet-lampe, l'objet reste toujours autant éclairé. Hors, bien évidemment, plus la lampe est loin de l'objet, moins la puissance est grande.
On va corriger ça, autant que faire ce peut.
Voilà notre schéma du jour:

La boule jaune, c'est la lumière, et en bas, c'est le calque.
Alors on pourrait se dire :
"Et bah on assimiler la distance lampe-calque à la "diffuse" du calque !"
C'est en effet ce que l'on va faire, mais il y a un léger hic. AE éclaire le calque de manière uniforme (sans prendre en compte le spéculaire). Imaginez que la lampe se déplace sur le plan parallele au calque (donc là sur l'axe XY), la distance lampe-calque va augmenter.
Hors, si le calque fait 2000x2000, et que la le calque se déplace de 1000 sur X, la lumière va baisser (car la distance augmente), alors que la lumière est toujours "au dessus" du calque.
Nous allons donc séparer la distance Z, et la distance XY (la ligne jaune au sol)
Aller c'est parti.
Créons un calque Null de control, qui va nous permettre de regler l'atténuation. Ajoutez 2 paramètre glissère, "début" et "fin"
Créez également une lumière "point".
Créez un 1er calque 3d, aller dans le paramètre diffuse, et écrivez :
a=position; b=thisComp.layer("Lumière 1").transform.position;
debut=thisComp.layer("controle lumiere").effect("debut")("Curseur");
fin=thisComp.layer("controle lumiere").effect("fin")("Curseur");
J'explique pas.
La suite:
V=sub(b,a);
Vec=fromWorldVec(V);
La 1ere ligne, vous connaissez, on crée un vecteur de a vers b.
Pour la 2eme, je m'explique.
Voyez sur le dessin la ligne orange, le vecteur. C'est un vecteur qui appartient à l'espace général de AE. Nous avons besoin que ce vecteur soit regardé par le calque, pour pouvoir séparer Z,X et Y. C'est le role de fromWorldVec. On change de référenciel, du "monde" vers le calque.
On se libère ainsi des valeurs de rotation du calque.
distanceZ=Math.abs(Vec[2]);
On récupère ainsi la composante Z du vecteur. Si on avait faire ça avec V et non Vec, la composante Z ([2]) aurait été celle du monde AE, qu'importe l'angle du calque.
Le math.abs permet d'éviter le probleme d'orientation du calque.
Voilà, on a crée une valeur qui donne la distance perpendiculaire du calque vers la lampe.
valz=ease(distanceZ,debut,fin,value,0);
Là on a crée la valeur de la diffuse en fonction de distanceZ.
Vous comprenez ainsi que la valeur "début" doit correspondre au début de l'atténuation, et "fin" doit correspondre à la distance où le calque sera noir.
Passons à l'atténuation sur le plan parallèle au calque, le plan XY.
On va faire en sorte que la déperdition commence à début+"en gros la taille du calque". Ainsi, si début=0, l'atténuation commencera quand la lampe "sortira" du calque.
distanceM=(width+height)/4;
distanceXY=Math.abs ( add(Vec[0],Vec[1]) );
valXY=ease(distanceXY,debut+distanceM,fin+distanceM,value,0);
On crée donc une variable très approximative (mais ça fonctionne pas trop mal).
C'est donc la moyenne entre la largeur et la hauteur du calque (width+height)/2, que je redivise par 2, pour n'avoir que la moitié. En effet, on considèrera que le point d'ancrage est au milieu du calque.
Ensuite, on crée la longueur du trait jaune (sur le dessin), c'est à dire la projection du vecteur sur le calque. "add" fait l'addition de 2 vecteurs. Regardez le dessin, on voit bien que x+y=trait jaune.
Ensuite, on fait la même chose que pour Z, mais avec XY. C'est pour cela qu'on rajoute distanceM à début et fin, pour tout décaler.
La dernière ligne :
Math.pow(valz*valXY,.5);
C'est donc la multiplication des 2 valeurs crées, le tout à la racine carrée.
Ainsi, on reste au maximum à 50, et quand une des 2 valeurs est à 0, le tout est bien à 0.
On peut évidemment remplacer les 0 par une valeur positive, pour ne jamais avoir de calque noir.
Voilà, ça aide un peu, ça a ses limites... Si vous voulez utiliser une valeur spéculaire pour le calque, copier l'expression également dedans.
Aller, l'expression en entier :
a=position; b=thisComp.layer("Lumière 1").transform.position;
debut=thisComp.layer("controle lumiere").effect("debut")("Curseur");
fin=thisComp.layer("controle lumiere").effect("fin")("Curseur");
V=sub(b,a);
Vec=fromWorldVec(V);
distanceZ=Math.abs(Vec[2]);
valz=ease(distanceZ,debut,fin,value,0);
distanceM=(width+height)/4;
distanceXY=Math.abs ( add(Vec[0],Vec[1]) );
valXY=ease(distanceXY,debut+distanceM,fin+distanceM,value,0);
valeur=Math.pow(valz*valXY,.5);
Ca marche avec une seule lampe, c'est compliqué de le faire avec plusieurs lampes pour plusieurs raison :
On utilise un gros système D, qui fait que le calque devient lui meme plus sombre selon la distance de la lampe. Donc s'il y a une lampe rouge et une lampe bleue, et que la lampe bleu est loin, et la lampe rouge, ça ne marche pas : le calque sera bien éclairé car la rouge est proche, mais le calque sera donc violet, à cause de la lumière bleue.
Voilà, j'espère avoir été clair !
Plus début et fin sont petits, plus l effet sera fort.
Rechargez la page pour que les 2 animations soient syncrho.
avec:

sans:

un autre exemple, notez dans le "avec" le coin supérieur gauche qui s'assombri, et évidemment, tout devient noir quand la lumière monte trop haut.
jeudi 26 mars 2009
pouet pouet
Aller, un petit truc truc simple !

L'idée est la suivante :
Qu'importe la méthode pour bouger le carré, il se déforme tout seul quand il touche le sol.
Pour ça, nous allons non pas bouger le carré lui même, mais un Null.
Ensuite, on dira ceci au carré :
Tu suis le Null dans sa position, mais si ta position en Y atteint une certaine valeur, tu ne bouges sur Y.
On va déjà faire ça.
Créez un Null, et un petit carré. Rajoutez à ce petit carré un paramètre glissière, et nommez le "sol". Mettez y 350 (ma compo fait 480x360, je vous rappelle que 350, c'est en bas).
Dans le point d'ancrage du carré, corrigez Y pour qu'il soit en bas. Si votre carré fait 50x50, vous aurez donc [25,50].
Dans la position du carré, on va écrire ça :
N=thisComp.layer("Nul 1").transform.position; //position du Null
sol=effect("sol")("Curseur"); //valeur de "sol"
Y=Math.min(N[1],sol); // On dit que Y vaut la valeur minimum entre le y du Null, et la valeur de sol. Ainsi, quand le y du Null vaut plus que 350 (plus bas donc), Y garde la valeur du sol.
[N[0],Y] // On veut que le carré ait la valeur de x du Null pour x, et Y pour y.
Bougez votre Null, le carré ne descendra pas sous la valeur du sol.
C'était quand même pas sorcier.
Passons à la déformation.
Voilà ce qu'on va dire au carré.
Plus tu es loin du Null, plus ton échelle sur X augmente, et plus ton échelle sur Y diminue.
Tout d'abord, rajoutez un paramètre glissière au carré, et nommez le "facteur", avec 3 comme valeur.
Écrivez dans l'échelle du carré :
p=position;
N=thisComp.layer("Nul 1").transform.position;
w=width;
F=effect("facteur")("Curseur");
Même pas mal.
Ensuite :
dist=p[1]-N[1];
Voilà, comme ça, on a une variable qui donne la distance verticale entre le carré et le Null. J'aurais même pu écrire dist=length(p,N), puisque de toute manière, ils ont toujours le même X.
Ca fonctionne car quand le carré est en l'air, dist vaut forcément 0 puisqu'il suit le Null. Mais quand il est au sol, c'est à ce moment que le Null se sépare du carré, et que dist prend une valeur non nulle.
x=linear(dist,-w/2,0,F*100,100);
y=linear(dist,-w/2,0,100/F,100);
Ca a l'air compliqué comme ça, mais en fait, non.
C'est simple, on veut ceci:
Plus le Null est loin, plus la déformation se fait.
Quand Null s'éloigne du carré, son Y est plus grand que celui du carré. Donc dist devient négatif.
C'est pour cela que j'ai choisi -w/2 comme distance de déformation : la moitié de la hauteur du carré. Ainsi, il suffit que le Null descende "d'un demi carré" pour que la déformation se fasse au maximum. C'est une valeur subjective, mais elle a le mérite d'être fonction de la taille du carré. On aurait pu aussi metre 2, 25 ou 250.
Et donc, quand dist=-w/2, et bien x=300, car nous avons mis 3 dans la valeur facteur.
Donc si on multiplie X par 3, on va diviser Y par 3.
D'où le 100/F, qui divise bien 100 par 3.
Et évidemment, la dernière ligne :
[x,y]
Et voilà, vous pouvez tester, ça fonctionne, plus le "facteur" est grand, plus la déformation sera grande (3 c'est déjà pas mal)
Vous remarquerez une finesse, le carré fait de légère rotation. Nous voulons évidemment que les rotations se fassent uniquement en l'air, et non quand le carré est au sol.
Pour la rotation :
haut=100;
bas=300;
F=ease(position[1],haut,bas,60,0);
wiggle(2,F)
En dessous de 300, la rotation vaut 0, et elle augmente quand y va de 300 jusqu à 100. Au delà de 100, elle se maintient.
Il ne reste plus qu'à bruiter tout ça, avec gout.
Pour que la hauteur du son varie, j'ai activé le remappage temporel pour chaque son, en mettant ça dans l'expression :
seedRandom(index,true);
max=thisComp.layer("Nul 1").effect("son max")("Curseur");
min=thisComp.layer("Nul 1").effect("son min")("Curseur");
R=random(min,max);
(time-inPoint)*R
max vaut 1.5 et min vaut 0.5
Ainsi, chaque son va à sa propre vitesse.
Pourquoi time-inPoint ?
time est fonction de la compo, pas de chaque calque.
Ainsi, si un calque commence à la seconde 5, à sa première image, time vaudra 5.
donc comme on veut partir de 0, on rajoute - inPoint (qui vaut la valeur du temps au début du calque)
C'est un moyen simple pour avoir la valeur de temps en partant de 0 au début du calque.
Petite astuce :
Sur ces deux animations, le mouvement du Null a été fait par dessin de trajectoire, et en m'appliquant à la souris pour faire un truc qui ressemble à quelque chose.
Toutefois, il n'est pas évident sur ce type de mouvement de s'arrêter en bas au bon endroit:
Si vous descendez trop, le carré va rester trop longtemps écrasé. Et si vous ne descendez pas assez, il ne vas pas être écrasé assez longtemps.
Voilà comment j'ai fait :
J'ai fait mon mouvement, ensuite j'ai sélectionné toutes les clefs de position crées, et je les ai déplacées pour que les clefs du bas soit au bon endroit.

L'idée est la suivante :
Qu'importe la méthode pour bouger le carré, il se déforme tout seul quand il touche le sol.
Pour ça, nous allons non pas bouger le carré lui même, mais un Null.
Ensuite, on dira ceci au carré :
Tu suis le Null dans sa position, mais si ta position en Y atteint une certaine valeur, tu ne bouges sur Y.
On va déjà faire ça.
Créez un Null, et un petit carré. Rajoutez à ce petit carré un paramètre glissière, et nommez le "sol". Mettez y 350 (ma compo fait 480x360, je vous rappelle que 350, c'est en bas).
Dans le point d'ancrage du carré, corrigez Y pour qu'il soit en bas. Si votre carré fait 50x50, vous aurez donc [25,50].
Dans la position du carré, on va écrire ça :
N=thisComp.layer("Nul 1").transform.position; //position du Null
sol=effect("sol")("Curseur"); //valeur de "sol"
Y=Math.min(N[1],sol); // On dit que Y vaut la valeur minimum entre le y du Null, et la valeur de sol. Ainsi, quand le y du Null vaut plus que 350 (plus bas donc), Y garde la valeur du sol.
[N[0],Y] // On veut que le carré ait la valeur de x du Null pour x, et Y pour y.
Bougez votre Null, le carré ne descendra pas sous la valeur du sol.
C'était quand même pas sorcier.
Passons à la déformation.
Voilà ce qu'on va dire au carré.
Plus tu es loin du Null, plus ton échelle sur X augmente, et plus ton échelle sur Y diminue.
Tout d'abord, rajoutez un paramètre glissière au carré, et nommez le "facteur", avec 3 comme valeur.
Écrivez dans l'échelle du carré :
p=position;
N=thisComp.layer("Nul 1").transform.position;
w=width;
F=effect("facteur")("Curseur");
Même pas mal.
Ensuite :
dist=p[1]-N[1];
Voilà, comme ça, on a une variable qui donne la distance verticale entre le carré et le Null. J'aurais même pu écrire dist=length(p,N), puisque de toute manière, ils ont toujours le même X.
Ca fonctionne car quand le carré est en l'air, dist vaut forcément 0 puisqu'il suit le Null. Mais quand il est au sol, c'est à ce moment que le Null se sépare du carré, et que dist prend une valeur non nulle.
x=linear(dist,-w/2,0,F*100,100);
y=linear(dist,-w/2,0,100/F,100);
Ca a l'air compliqué comme ça, mais en fait, non.
C'est simple, on veut ceci:
Plus le Null est loin, plus la déformation se fait.
Quand Null s'éloigne du carré, son Y est plus grand que celui du carré. Donc dist devient négatif.
C'est pour cela que j'ai choisi -w/2 comme distance de déformation : la moitié de la hauteur du carré. Ainsi, il suffit que le Null descende "d'un demi carré" pour que la déformation se fasse au maximum. C'est une valeur subjective, mais elle a le mérite d'être fonction de la taille du carré. On aurait pu aussi metre 2, 25 ou 250.
Et donc, quand dist=-w/2, et bien x=300, car nous avons mis 3 dans la valeur facteur.
Donc si on multiplie X par 3, on va diviser Y par 3.
D'où le 100/F, qui divise bien 100 par 3.
Et évidemment, la dernière ligne :
[x,y]
Et voilà, vous pouvez tester, ça fonctionne, plus le "facteur" est grand, plus la déformation sera grande (3 c'est déjà pas mal)
Vous remarquerez une finesse, le carré fait de légère rotation. Nous voulons évidemment que les rotations se fassent uniquement en l'air, et non quand le carré est au sol.
Pour la rotation :
haut=100;
bas=300;
F=ease(position[1],haut,bas,60,0);
wiggle(2,F)
En dessous de 300, la rotation vaut 0, et elle augmente quand y va de 300 jusqu à 100. Au delà de 100, elle se maintient.
Il ne reste plus qu'à bruiter tout ça, avec gout.
Pour que la hauteur du son varie, j'ai activé le remappage temporel pour chaque son, en mettant ça dans l'expression :
seedRandom(index,true);
max=thisComp.layer("Nul 1").effect("son max")("Curseur");
min=thisComp.layer("Nul 1").effect("son min")("Curseur");
R=random(min,max);
(time-inPoint)*R
max vaut 1.5 et min vaut 0.5
Ainsi, chaque son va à sa propre vitesse.
Pourquoi time-inPoint ?
time est fonction de la compo, pas de chaque calque.
Ainsi, si un calque commence à la seconde 5, à sa première image, time vaudra 5.
donc comme on veut partir de 0, on rajoute - inPoint (qui vaut la valeur du temps au début du calque)
C'est un moyen simple pour avoir la valeur de temps en partant de 0 au début du calque.
Petite astuce :
Sur ces deux animations, le mouvement du Null a été fait par dessin de trajectoire, et en m'appliquant à la souris pour faire un truc qui ressemble à quelque chose.
Toutefois, il n'est pas évident sur ce type de mouvement de s'arrêter en bas au bon endroit:
Si vous descendez trop, le carré va rester trop longtemps écrasé. Et si vous ne descendez pas assez, il ne vas pas être écrasé assez longtemps.
Voilà comment j'ai fait :
J'ai fait mon mouvement, ensuite j'ai sélectionné toutes les clefs de position crées, et je les ai déplacées pour que les clefs du bas soit au bon endroit.
rubrique:
expressions after effect ecraser squeeze
dimanche 22 mars 2009
plein et délier
Comme je suis généreux, on va voir encore un petit truc... Franchement vous allez voir, c'est vraiment pas mal.
Certains d'entre vous connaisse peut etre l'effet "tracé dynamique" ("write on" en anglais je crois)
On anime un point dans sa position, et ça dessine un trait. On peut évidemment attacher ce point à un objet pour que ce dernier laisse un tracé, etc, ça sert à plein de choses.
Mais ici, on va faire un truc chouette, on va gérer les pleins et les déliers. Telle une plume, selon la direction du dessin, l'épaisseur sera différente. On évite ainsi le feutre rond qui ne change jamais de taille.

Voilà ce que nous allons faire :
Il faut que le diamètre varie selon la direction du tracé.
Donc tout le problème est là, trouver l'angle qui définit la direction du tracé.
C'est parti,
Créez un solide plein pot dans la compo, et ajouter l'effet "tracé dynamique".
Comme nous allons faire varier le diamètre DANS LE TEMPS, dans "tracé dans le temps", choisissez "épaisseur"
Rajoutez 3 paramètres glissières "angle", "min" et "max"
angle va représenter l'angle de la plume. Rentrez par 40 degré.
Dans min, mettez 3, et 20 pour max.
Nous allons maintenant créer une expression dans "épaisseur" dans l'effet "tracé dynamique".
taillemax=effect("max")("Curseur");
taillemin=effect("min")("Curseur");
angleplume=effect("angle")("Curseur");
J'explique meme pas, ça serait une insulte pour vous.
On passe au coeur du problème, la direction du tracé.
Voilà comment on va faire :
Nous allons récupérer 2 positions :
-Celle à l'image N
-celle à l'image N-1
En créant un vecteur qui va d'un point à l'autre, on a bien la direction !
C'est parti.
pos=effect("Tracé dynamique")("Position");
d=thisComp.frameDuration;
posd=pos.valueAtTime(time-d);
Alors...
pos, c'est la position du point à l'image courante.
On crée d, qui correspond à la valeur temporelle d'une image. Par exemple, si vous ètes à 25i/s, d=1/25
Enuite, posd correspond à la position, mais une image avant (time-d).
vecteur=sub(pos,posd);
Hop, ça c'est le vecteur.
vari=radiansToDegrees(Math.atan2(vecteur[1],vecteur[0]));
Exactement ce qu'on a vu dans le post précédent, on trouve l'angle en décomposant le vecteur.
Ici, vous remarquez une nuance, au lieu d'avoir Math.atan (coté opp/coté adj), j'ai Math.atan2(coté opp, coté adj), on peut faire les deux.
Voilà, on a récupéré la direction du tracé !
taille=Math.sin(degreesToRadians(vari + angleplume));
Et là, on chope le sinus de l'angle. on part de l'angle de la plume ecrit dans le paramètre glissère (40 là)+la variation dans le temp de la direction. On ainsi taille qui varie de -1 à 1.
On va utiliser sa valeur absolue pour que ça varie de 0 à 1.
Dernière ligne :
Math.abs(taille)*taillemax + taillemin
C'est ici qu'on a la valeur de l'épaisseur. On multiplie donc la valeur absolue de taille (qui varie entre 0 et 1) à taillemax, le tout additionné à taillemin, qui est l'épaisseur minimum.
Ainsi, selon l'angle, taillemax se rajoutera à taillemin, addition de 0 à 20 ici.
Et voilà !!!
vous pouvez également animer les valeurs taillemin et taillemax dans le temps, ça marche.
Vous pouvez rajouter un wiggle à la position ou à l'épaisseur, etc.
Il y a différentes façon de créer une trajectoire.
Avec des clefs, en s'accrochant à un objet sur lequel on a effectué un dessin de trajectoire, en collant un masque dans la position qui se transforme en position, etc.
Merci la trigo.
Certains d'entre vous connaisse peut etre l'effet "tracé dynamique" ("write on" en anglais je crois)
On anime un point dans sa position, et ça dessine un trait. On peut évidemment attacher ce point à un objet pour que ce dernier laisse un tracé, etc, ça sert à plein de choses.
Mais ici, on va faire un truc chouette, on va gérer les pleins et les déliers. Telle une plume, selon la direction du dessin, l'épaisseur sera différente. On évite ainsi le feutre rond qui ne change jamais de taille.

Voilà ce que nous allons faire :
Il faut que le diamètre varie selon la direction du tracé.
Donc tout le problème est là, trouver l'angle qui définit la direction du tracé.
C'est parti,
Créez un solide plein pot dans la compo, et ajouter l'effet "tracé dynamique".
Comme nous allons faire varier le diamètre DANS LE TEMPS, dans "tracé dans le temps", choisissez "épaisseur"
Rajoutez 3 paramètres glissières "angle", "min" et "max"
angle va représenter l'angle de la plume. Rentrez par 40 degré.
Dans min, mettez 3, et 20 pour max.
Nous allons maintenant créer une expression dans "épaisseur" dans l'effet "tracé dynamique".
taillemax=effect("max")("Curseur");
taillemin=effect("min")("Curseur");
angleplume=effect("angle")("Curseur");
J'explique meme pas, ça serait une insulte pour vous.
On passe au coeur du problème, la direction du tracé.
Voilà comment on va faire :
Nous allons récupérer 2 positions :
-Celle à l'image N
-celle à l'image N-1
En créant un vecteur qui va d'un point à l'autre, on a bien la direction !
C'est parti.
pos=effect("Tracé dynamique")("Position");
d=thisComp.frameDuration;
posd=pos.valueAtTime(time-d);
Alors...
pos, c'est la position du point à l'image courante.
On crée d, qui correspond à la valeur temporelle d'une image. Par exemple, si vous ètes à 25i/s, d=1/25
Enuite, posd correspond à la position, mais une image avant (time-d).
vecteur=sub(pos,posd);
Hop, ça c'est le vecteur.
vari=radiansToDegrees(Math.atan2(vecteur[1],vecteur[0]));
Exactement ce qu'on a vu dans le post précédent, on trouve l'angle en décomposant le vecteur.
Ici, vous remarquez une nuance, au lieu d'avoir Math.atan (coté opp/coté adj), j'ai Math.atan2(coté opp, coté adj), on peut faire les deux.
Voilà, on a récupéré la direction du tracé !
taille=Math.sin(degreesToRadians(vari + angleplume));
Et là, on chope le sinus de l'angle. on part de l'angle de la plume ecrit dans le paramètre glissère (40 là)+la variation dans le temp de la direction. On ainsi taille qui varie de -1 à 1.
On va utiliser sa valeur absolue pour que ça varie de 0 à 1.
Dernière ligne :
Math.abs(taille)*taillemax + taillemin
C'est ici qu'on a la valeur de l'épaisseur. On multiplie donc la valeur absolue de taille (qui varie entre 0 et 1) à taillemax, le tout additionné à taillemin, qui est l'épaisseur minimum.
Ainsi, selon l'angle, taillemax se rajoutera à taillemin, addition de 0 à 20 ici.
Et voilà !!!
vous pouvez également animer les valeurs taillemin et taillemax dans le temps, ça marche.
Vous pouvez rajouter un wiggle à la position ou à l'épaisseur, etc.
Il y a différentes façon de créer une trajectoire.
Avec des clefs, en s'accrochant à un objet sur lequel on a effectué un dessin de trajectoire, en collant un masque dans la position qui se transforme en position, etc.
Merci la trigo.
rubrique:
expressions after effect ecriture delier
look me in 2d
Alors alors, comment faire pour qu'un calque en regarde un autre, ou du moins que sa rotation soit fonction de la position d'un autre.
Tout d'abord, reregardons ça:
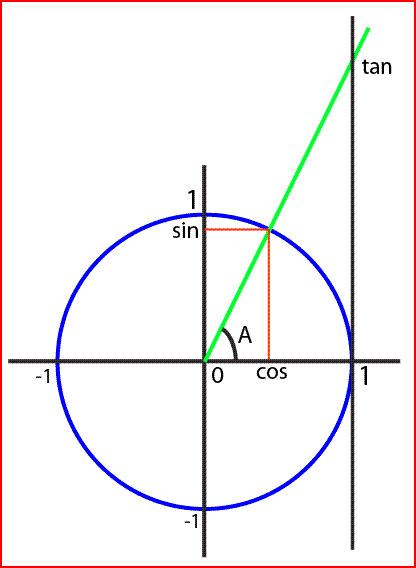
Imaginez que notre objet est sur le point 0, et que l'objet cible soit sur le point "tan", ou du moins sur l'axe de la ligne verte, ça revient au meme.
On cherche donc l'angle A.
Et bien on a cette formule :
tan(A)=coté opposé / coté adjacent.
Par coté adjacent, on parle du coté qui appartient à l'angle, est qui n'est pas la ligne verte (la ligne du cosinus donc, de 0 à 1)
Et par coté opposé, et bien c'est l'autre segment, celui qui n'appartient pas à l'angle (et toujours différent de la ligne verte), la ligne qui va donc de 1 à tan.
Passons à la pratique :
a=position;
b=thisComp.layer("Rouge sombre uni 1").transform.position;
Ca c'est simple, ce sont les deux variables de position. Celle du calque, et celle de la cible.
V=sub(b,a);
Là on crée le vecteur qui correspond à la ligne verte, la ligne qui va de a vers b.
radiansToDegrees ( Math.atan2 ( V[1],V[0] ))
Math.atan2 : il ne s'agit pas de la tangente, mais de la tangente dans le sens inverse.
Quand vous écrivez Math.tan(angle), ça vous donne la tangente de l'angle.
Math.atan2(tan), ça vous donne l'angle de la tangente.
Même chose pour avec Math.acos et Math.asin.
Petite finesse avec atan2, les deux "coté" sont séparés par une virgule.
Donc dans Math.atan2(), on doit inscrire la tangente, c'est donc coté opposé/coté adjacent.
C'est très simple, il suffit de prendre les composantes sur x et y du vecteur.
Reregardez le dessin, surtout la ligne verte. Le coté adjacent et le coté opposé corresponde bien aux composantes x et y de la ligne verte.
On note donc V[0] (sur x) et V[1] (sur y).
Et comme d'habitude, radiansToDegrees, car Math.atan2 donne un angle en radians.
Un petit exemple mixant plein de choses qu'on a vu, j'ai jamais dit que c'était joli.

On verra plus tard le coup de la taille qui change, mais vous avez les outils pour le faire.
Tout d'abord, reregardons ça:

Imaginez que notre objet est sur le point 0, et que l'objet cible soit sur le point "tan", ou du moins sur l'axe de la ligne verte, ça revient au meme.
On cherche donc l'angle A.
Et bien on a cette formule :
tan(A)=coté opposé / coté adjacent.
Par coté adjacent, on parle du coté qui appartient à l'angle, est qui n'est pas la ligne verte (la ligne du cosinus donc, de 0 à 1)
Et par coté opposé, et bien c'est l'autre segment, celui qui n'appartient pas à l'angle (et toujours différent de la ligne verte), la ligne qui va donc de 1 à tan.
Passons à la pratique :
a=position;
b=thisComp.layer("Rouge sombre uni 1").transform.position;
Ca c'est simple, ce sont les deux variables de position. Celle du calque, et celle de la cible.
V=sub(b,a);
Là on crée le vecteur qui correspond à la ligne verte, la ligne qui va de a vers b.
radiansToDegrees ( Math.atan2 ( V[1],V[0] ))
Math.atan2 : il ne s'agit pas de la tangente, mais de la tangente dans le sens inverse.
Quand vous écrivez Math.tan(angle), ça vous donne la tangente de l'angle.
Math.atan2(tan), ça vous donne l'angle de la tangente.
Même chose pour avec Math.acos et Math.asin.
Petite finesse avec atan2, les deux "coté" sont séparés par une virgule.
Donc dans Math.atan2(), on doit inscrire la tangente, c'est donc coté opposé/coté adjacent.
C'est très simple, il suffit de prendre les composantes sur x et y du vecteur.
Reregardez le dessin, surtout la ligne verte. Le coté adjacent et le coté opposé corresponde bien aux composantes x et y de la ligne verte.
On note donc V[0] (sur x) et V[1] (sur y).
Et comme d'habitude, radiansToDegrees, car Math.atan2 donne un angle en radians.
Un petit exemple mixant plein de choses qu'on a vu, j'ai jamais dit que c'était joli.

On verra plus tard le coup de la taille qui change, mais vous avez les outils pour le faire.
samedi 21 mars 2009
je mords pas
Si un post ne vous parait pas clair, ou si vous avez un besoin particulier pour une animation, n'hésite pas à laisser vos commentaires.
En général, les expressions naissent d'un besoin pratique, donc certains de vos besoins peuvent créer de nouveaux types de réponses.
Attention, pour les questions dont les réponses sont déjà sur le blog, j'envoie des décharges dans vos ports USB.
Comment faisiez vous avant les expressions ?... Franchement, c'était galère.
Maintenant, c'est galère aussi, mais pour d'autres raisons.
Et n'oubliez pas :
Si il y a quelque chose que je n'explique pas dans un post, ou bien que je survole, c'est que ça été forcément expliqué en long en large et en travers dans un post précédent.
En général, les expressions naissent d'un besoin pratique, donc certains de vos besoins peuvent créer de nouveaux types de réponses.
Attention, pour les questions dont les réponses sont déjà sur le blog, j'envoie des décharges dans vos ports USB.
Comment faisiez vous avant les expressions ?... Franchement, c'était galère.
Maintenant, c'est galère aussi, mais pour d'autres raisons.
Et n'oubliez pas :
Si il y a quelque chose que je n'explique pas dans un post, ou bien que je survole, c'est que ça été forcément expliqué en long en large et en travers dans un post précédent.
on fait une tomate ?
Il y a tellement de choses à faire avec la trigo, je ne sais pas par quoi continuer...(en fait, si, mais bon...)
Nous avons vu que nous pouvions faire évoluer un objet sur une trajectoire circulaire, ou bien en spirale si on fait évoluer le diamètre dans le temps.
Nous avons vu, au tout début du blog, que la fonction INDEX permet que chaque calque ait une constante différente de ces voisins en fonction de sa position dans la timeline.
Nous allons mixer ensemble trigo et index. (ça fait indigo !)
Plaçons plein de calques sur un cercle, ou un arc de cercle :

Ici, on fait évoluer le diamètre, l'angle, et la taille de l'arc.
Vous allez voir, c'est pas bien compliqué.
On commence par les classiques Null : un "plafond" et un "sol"( le sol en dessous évidemment merci).
Nous allons utiliser le Null "plafond" comme calque de contrôle.
Rajoutez 2 paramètres angle "angle" et "arc"
Rajoutez également un paramètre glissière "diamètre".
Rentrez d'ores et deja 120 dans arc, et 50 dans diamètre. Qu'importe les valeurs, pourvu que ça ne soit pas 0.
Créez un calque, qui sera le centre (ça peut aussi être un Null, ou meme le calque "plafond"(pensez à le passer en 3d si tout ça est en 3d), pour être invisible)
Créez un petit calque tout mignon, et ouvrez sa position, et c'est parti.
origine=thisComp.layer("centre").transform.position;
plafond=thisComp.layer("plafond").index;
I=index-plafond; nombre=thisComp.layer("sol").index-plafond-1;
angle=thisComp.layer("plafond").effect("angle")("Angle");
arc=thisComp.layer("plafond").effect("arc")("Angle");
diametre=thisComp.layer("plafond").effect("diametre")("Curseur");
Ça impressionne plein de gens, mais pas vous !
On a juste créé les variables que vous connaissez, on a vu récemment le coup de l'index entre plafond et sol, nombre, pour connaitre le nombre de calques, et les 3 variables du calque de contrôle.
pos=linear(I,1,nombre,0,1); // j'ai appelé la variable "pos" pour la position du calque dans la timeline. Je ne peux pas utiliser "position", c'est déjà pris.
Ca aussi vous connaissez. On attribut à chaque calque un nombre entre 0 et 1 en fonction de la position entre plafond et sol.
x= Math.cos ( degreesToRadians ( angle+arc*pos ) )*diametre;
y= Math.sin ( degreesToRadians ( angle+arc*pos ) )*diametre;
[x,y]+origine
Et voilà les dernières lignes.
On va juste voir "x", puisque pour "y", c'est la même chose à part le Math.sin.
Alors :
( angle+arc*pos ) Ca, c'est notre angle, en degré, de chaque calque. Il est donc égale à l'angle général, plus l'arc. Cette arc est multiplié par "pos", qui va de 0 à 1.
Donc on comprend que si angle vaut 25, et que arc vaut 90, pour le premier calque, l'angle total vaut 25, puisque 90*0=0, et le dernier calque vaudra 115.
Comme cet angle est en degré, on rajoute degreesToRadians pour que Math.cos lise bien un angle en radian à l'interieur de la parenthèse. Comme les cos et sin vont de -1 à 1, on multiplie le tout par le diamètre, pour avoir la distance voulue jusqu'au centre.
Voilà, comme ça, vous pourrez postuler chez TF1...
Dans mes 2 exemples, les variables angle, arc et diamètre sont animées. Ces variables ne sont pas forcément à animer, elles peuvent également être des variables d'ajustement. Imaginer la vidéo "qui veut gagner des expressions", avec une camera au mileu des lumières. Vous n'allez donc que placer les lumières que la camera verra. Ensuite, en fonction des mouvements de camera et de sa focale, vous allez pouvoir régler l'espacement et le nombre de lumière en un rien de temps. Vous pourrez ainsi ajuster votre scène à loisir.
Dans l'animation avec les petits carrés, ils sont bien autour du centre, mais la rotation ne change pas. On peut biensur faire en sorte qu'ils soient tous orientés vers le centre. Au moins, on a le choix, contrairement à la technique "décalage du point d'ancrage et utilisation de la rotation".
Si votre calque est en 3d, vous vous en doutez, ils vous suffit d'utiliser lookAt dans l'orientation.
Et kesako si votre calque est un calque 2d, et que pour diverses raisons, vous ne pouvez pas le passer en 3d ? Comment orienter votre calque ?
Il y a toujours la solution de l'orientation automatique, mais celle ci ne fonctionne que quand le calque se déplace.
Nous verrons dans le prochain post comment faire pour qu'un calque 2d soit orienté par rapport à un autre calque.
Nous avons vu que nous pouvions faire évoluer un objet sur une trajectoire circulaire, ou bien en spirale si on fait évoluer le diamètre dans le temps.
Nous avons vu, au tout début du blog, que la fonction INDEX permet que chaque calque ait une constante différente de ces voisins en fonction de sa position dans la timeline.
Nous allons mixer ensemble trigo et index. (ça fait indigo !)
Plaçons plein de calques sur un cercle, ou un arc de cercle :

Ici, on fait évoluer le diamètre, l'angle, et la taille de l'arc.
Vous allez voir, c'est pas bien compliqué.
On commence par les classiques Null : un "plafond" et un "sol"( le sol en dessous évidemment merci).
Nous allons utiliser le Null "plafond" comme calque de contrôle.
Rajoutez 2 paramètres angle "angle" et "arc"
Rajoutez également un paramètre glissière "diamètre".
Rentrez d'ores et deja 120 dans arc, et 50 dans diamètre. Qu'importe les valeurs, pourvu que ça ne soit pas 0.
Créez un calque, qui sera le centre (ça peut aussi être un Null, ou meme le calque "plafond"(pensez à le passer en 3d si tout ça est en 3d), pour être invisible)
Créez un petit calque tout mignon, et ouvrez sa position, et c'est parti.
origine=thisComp.layer("centre").transform.position;
plafond=thisComp.layer("plafond").index;
I=index-plafond; nombre=thisComp.layer("sol").index-plafond-1;
angle=thisComp.layer("plafond").effect("angle")("Angle");
arc=thisComp.layer("plafond").effect("arc")("Angle");
diametre=thisComp.layer("plafond").effect("diametre")("Curseur");
Ça impressionne plein de gens, mais pas vous !
On a juste créé les variables que vous connaissez, on a vu récemment le coup de l'index entre plafond et sol, nombre, pour connaitre le nombre de calques, et les 3 variables du calque de contrôle.
pos=linear(I,1,nombre,0,1); // j'ai appelé la variable "pos" pour la position du calque dans la timeline. Je ne peux pas utiliser "position", c'est déjà pris.
Ca aussi vous connaissez. On attribut à chaque calque un nombre entre 0 et 1 en fonction de la position entre plafond et sol.
x= Math.cos ( degreesToRadians ( angle+arc*pos ) )*diametre;
y= Math.sin ( degreesToRadians ( angle+arc*pos ) )*diametre;
[x,y]+origine
Et voilà les dernières lignes.
On va juste voir "x", puisque pour "y", c'est la même chose à part le Math.sin.
Alors :
( angle+arc*pos ) Ca, c'est notre angle, en degré, de chaque calque. Il est donc égale à l'angle général, plus l'arc. Cette arc est multiplié par "pos", qui va de 0 à 1.
Donc on comprend que si angle vaut 25, et que arc vaut 90, pour le premier calque, l'angle total vaut 25, puisque 90*0=0, et le dernier calque vaudra 115.
Comme cet angle est en degré, on rajoute degreesToRadians pour que Math.cos lise bien un angle en radian à l'interieur de la parenthèse. Comme les cos et sin vont de -1 à 1, on multiplie le tout par le diamètre, pour avoir la distance voulue jusqu'au centre.
Voilà, comme ça, vous pourrez postuler chez TF1...
Dans mes 2 exemples, les variables angle, arc et diamètre sont animées. Ces variables ne sont pas forcément à animer, elles peuvent également être des variables d'ajustement. Imaginer la vidéo "qui veut gagner des expressions", avec une camera au mileu des lumières. Vous n'allez donc que placer les lumières que la camera verra. Ensuite, en fonction des mouvements de camera et de sa focale, vous allez pouvoir régler l'espacement et le nombre de lumière en un rien de temps. Vous pourrez ainsi ajuster votre scène à loisir.
Dans l'animation avec les petits carrés, ils sont bien autour du centre, mais la rotation ne change pas. On peut biensur faire en sorte qu'ils soient tous orientés vers le centre. Au moins, on a le choix, contrairement à la technique "décalage du point d'ancrage et utilisation de la rotation".
Si votre calque est en 3d, vous vous en doutez, ils vous suffit d'utiliser lookAt dans l'orientation.
Et kesako si votre calque est un calque 2d, et que pour diverses raisons, vous ne pouvez pas le passer en 3d ? Comment orienter votre calque ?
Il y a toujours la solution de l'orientation automatique, mais celle ci ne fonctionne que quand le calque se déplace.
Nous verrons dans le prochain post comment faire pour qu'un calque 2d soit orienté par rapport à un autre calque.
rubrique:
after effect expression rang cercle
vendredi 20 mars 2009
c'est pas compliqué pourtant...
jeudi 19 mars 2009
gestion multi couleurs
Je fais une parenthèse pendant la trigo, voilà un post que j'avais oublié de poster.
On a vu comment gérer une meme couleur sur plusieurs calques à la fois ici :
http://lefreelancesaucisse.blogspot.com/2008/03/expressions-gestion-dune-couleur.html
Voyons comment gérer plusieurs couleurs pour plusieurs calques.
Par exemple, on veut créer plein de petits carrés, chaque carré prenant une couleur au hasard parmi nos 3 couleurs définies au préalable.

Créez un Null de control que nous appellerons "control couleurs"
Ajouter lui 3 effets "paramètre couleur"
Appliquez leur à chacun la couleur de votre choix.
Ajoutez également un paramètre glissière, votre ami de longue date. Appelez le "nombre"
Mettez 3 dans la valeur de "nombre", qui correspond donc au nombre de couleurs. Évidemment, si vous changez le nombre de couleurs, ce nombre doit changer aussi. Attention ! Si vous avez 4 couleurs, et que vous mettez 10, toutes les expressions vont s'annuler, car AE va vous dire qu'il n y a pas de 10eme effet dans le calque de contrôle.
Créez votre petit calque carré. Appliquez lui l'effet "remplir"
Nous allons créer une expression pour la couleur appliquée à "remplir"
Ce que nous voulons, c'est que le carré prenne une des 3 couleurs au hasard.
Déterminons deja le nombre de couleur:
max=thisComp.layer("control couleurs").effect("nombre")("Curseur");
Ensuite, on va définir le nombre qui va varier de 1 à 3, pour choisir un des 3 effets au hasard:
seedRandom(5,true);
R=random(1,max);
seedRandom(x,y), vous connaissez. x définit quelle présérie de chiffres aléatoires va etre utilisée, y (égale à true ou false) définit si le random sera fixe (true) ou bien changera à chaque frame (false) Là j'ai mis 5 comme j'aurais pu mettre 2, 15265, ou Math.PI. Qu'importe, c'est juste un nombre. Tous les calques auront donc ce 5, mais comme ce sont des calques différents, il n'auront pas la meme suite de chiffres.
Ainsi, R varie de 1 à 3.
La dernière ligne :
thisComp.layer("control couleurs").effect(R)("Couleur")
notez le R. Pour écrire cette phrase, faites comme d'habitude, prenez votre corde, et aller chercher par exemple la couleur du 1er effet "paramètre couleur"
Vous aurez ainsi une ligne qui ressemble à ça :
thisComp.layer("control couleurs").effect("Paramètre couleurs")("Couleur")
Dans la parenthèse de effect, vous avez, comme d'habitude, le nom de l'effet.
Nous l'avons donc remplacer par R, sans les "" donc. R joue ainsi le rôle d'index :
Va cherche l'effet qui est en R position.
Ainsi, il va chercher la couleur qui est dans l'effet 1,2 ou 3.
Si vous testez ça, vous vous rendrez compte que vous n'aurez quasiment jamais un carré de la 3eme couleur. C'est normal :
Imaginez une segment qui va de 1 à 3. AE va arrondir la valeur du random pour avoir une valeur entière...peu de chance d'avoir le chiffre 3 !
donc on va plutot écrire ça :
R=Math.ceil ( random(0,max));
Pour rappel, Math.ceil(x) donnc la valeur entière supérieure à x.
Math.ceil(1.2)=2
Math.ceil(3.9)=4
etc
Donc là, on force R à avoir la valeur entière supérieure. C'est pour cela que j'ai remplacé (1,max) par (0,max).
Ainsi, les 3 valeurs ont autant de chance de tomber que les autres :
de 0 à 1, R=1
de 1.01 à 2, R=2
de 2.01 à 3, R=3
L'expression finale :
max=thisComp.layer("control couleurs").effect("nombre")("Curseur")
seedRandom(5,true);
R=Math.ceil ( random(0,max));
thisComp.layer("control couleurs").effect(R)("Couleur")
si on écrit :
seedRandom(index,true);
Chaque calque changera de couleur quand il changera de position dans la timeline, ou dès qu'on rajoutera un calque dans la composition.
Et voilà !
Petite précision tout de même:
Une succession de valeurs aléatoires ne signifie pas homogénéité. Ca n'est pas la meme chose.
Pour chaque calque, chaque couleur a autant de chance de sortir qu'une autre, même si elle vient de sortir. Vous pouvez donc vous trouver avec 4 calques verts, ou bien 1 rouge et 3 bleus.
C'est comme pile ou face.
pile/face/pile/face/pile face n'est pas plus probable que
pile/pile/pile/face/pile
Ces 2 séries ont toutes les deux 1 chance sur 32 de sortir.
L'homogénéité sera visible avec un grand nombre de calques.
Ce principe ne sert évidemment pas qu'à remplir des calques, il peut aussi servir pour teinter des calques, ou je ne sais quoi...
On a vu comment gérer une meme couleur sur plusieurs calques à la fois ici :
http://lefreelancesaucisse.blogspot.com/2008/03/expressions-gestion-dune-couleur.html
Voyons comment gérer plusieurs couleurs pour plusieurs calques.
Par exemple, on veut créer plein de petits carrés, chaque carré prenant une couleur au hasard parmi nos 3 couleurs définies au préalable.

Créez un Null de control que nous appellerons "control couleurs"
Ajouter lui 3 effets "paramètre couleur"
Appliquez leur à chacun la couleur de votre choix.
Ajoutez également un paramètre glissière, votre ami de longue date. Appelez le "nombre"
Mettez 3 dans la valeur de "nombre", qui correspond donc au nombre de couleurs. Évidemment, si vous changez le nombre de couleurs, ce nombre doit changer aussi. Attention ! Si vous avez 4 couleurs, et que vous mettez 10, toutes les expressions vont s'annuler, car AE va vous dire qu'il n y a pas de 10eme effet dans le calque de contrôle.
Créez votre petit calque carré. Appliquez lui l'effet "remplir"
Nous allons créer une expression pour la couleur appliquée à "remplir"
Ce que nous voulons, c'est que le carré prenne une des 3 couleurs au hasard.
Déterminons deja le nombre de couleur:
max=thisComp.layer("control couleurs").effect("nombre")("Curseur");
Ensuite, on va définir le nombre qui va varier de 1 à 3, pour choisir un des 3 effets au hasard:
seedRandom(5,true);
R=random(1,max);
seedRandom(x,y), vous connaissez. x définit quelle présérie de chiffres aléatoires va etre utilisée, y (égale à true ou false) définit si le random sera fixe (true) ou bien changera à chaque frame (false) Là j'ai mis 5 comme j'aurais pu mettre 2, 15265, ou Math.PI. Qu'importe, c'est juste un nombre. Tous les calques auront donc ce 5, mais comme ce sont des calques différents, il n'auront pas la meme suite de chiffres.
Ainsi, R varie de 1 à 3.
La dernière ligne :
thisComp.layer("control couleurs").effect(R)("Couleur")
notez le R. Pour écrire cette phrase, faites comme d'habitude, prenez votre corde, et aller chercher par exemple la couleur du 1er effet "paramètre couleur"
Vous aurez ainsi une ligne qui ressemble à ça :
thisComp.layer("control couleurs").effect("Paramètre couleurs")("Couleur")
Dans la parenthèse de effect, vous avez, comme d'habitude, le nom de l'effet.
Nous l'avons donc remplacer par R, sans les "" donc. R joue ainsi le rôle d'index :
Va cherche l'effet qui est en R position.
Ainsi, il va chercher la couleur qui est dans l'effet 1,2 ou 3.
Si vous testez ça, vous vous rendrez compte que vous n'aurez quasiment jamais un carré de la 3eme couleur. C'est normal :
Imaginez une segment qui va de 1 à 3. AE va arrondir la valeur du random pour avoir une valeur entière...peu de chance d'avoir le chiffre 3 !
donc on va plutot écrire ça :
R=Math.ceil ( random(0,max));
Pour rappel, Math.ceil(x) donnc la valeur entière supérieure à x.
Math.ceil(1.2)=2
Math.ceil(3.9)=4
etc
Donc là, on force R à avoir la valeur entière supérieure. C'est pour cela que j'ai remplacé (1,max) par (0,max).
Ainsi, les 3 valeurs ont autant de chance de tomber que les autres :
de 0 à 1, R=1
de 1.01 à 2, R=2
de 2.01 à 3, R=3
L'expression finale :
max=thisComp.layer("control couleurs").effect("nombre")("Curseur")
seedRandom(5,true);
R=Math.ceil ( random(0,max));
thisComp.layer("control couleurs").effect(R)("Couleur")
si on écrit :
seedRandom(index,true);
Chaque calque changera de couleur quand il changera de position dans la timeline, ou dès qu'on rajoutera un calque dans la composition.
Et voilà !
Petite précision tout de même:
Une succession de valeurs aléatoires ne signifie pas homogénéité. Ca n'est pas la meme chose.
Pour chaque calque, chaque couleur a autant de chance de sortir qu'une autre, même si elle vient de sortir. Vous pouvez donc vous trouver avec 4 calques verts, ou bien 1 rouge et 3 bleus.
C'est comme pile ou face.
pile/face/pile/face/pile face n'est pas plus probable que
pile/pile/pile/face/pile
Ces 2 séries ont toutes les deux 1 chance sur 32 de sortir.
L'homogénéité sera visible avec un grand nombre de calques.
Ce principe ne sert évidemment pas qu'à remplir des calques, il peut aussi servir pour teinter des calques, ou je ne sais quoi...
mercredi 18 mars 2009
trigolo, oscillation
On a vu rapidement le début de l'utilisation de la trigo dans les expressions dans AE.
voyons à présent une autre utilisation citée précédemment, l'oscillation.
Comme nous l'avons vu, quand une valeur évolue de manière linéaire, son cos et son sin oscillent entre -1 et 1. Je parle de valeur et non d'angle, car finalement, on se fiche qu'il s'agisse d'un angle ou pas. Un angle est une valeur, donc n'importe quelle valeur a son cos et son sin.
Alors voilà, nous voulons faire osciller un petit baton de droite à gauche, comme ceci :

On le comprend, la valeur de rotation ici correspond au cos (ou au sin) d'un angle qui évolue de manière linéaire. Nous allons donc créer la valeur d'un angle fictif :
cercle=Math.PI*2;
hop, on a crée un constante qui correspond au périmètre du cercle (c'est une bonne habitude pour etre précis dans ce qu'on fait) freq=2;
ça, ça va etre le nombre de tour à la seconde que fait notre angle.
amp=40;
ça, ça va etre l'amplitude non pas de cet angle, mais de celui que nous appliquerons au final au haricot bio.
Math.cos(time*cercle*freq)*amp
et ça, c'est la dernière phrase.
Dans le Math.cos, on a bien notre angle en radian qui évolue, qui effectue un tour de périmètre (cercle) tous les tours (time), multiplié par 2 (freq), le tout, multiplié par amp.
Attention !! amp multiplie bien l'ensemble du Math.cos, et non pas à l'interieur de la parenthèse. Souvenez vous, le cos et le sin n'évoluent que de -1 à 1. Avec le amp à 40, le haricot bio va de -40 à 40.
Maintenant, nous voulons que le haricot bio soit freiné par l'air, et s'arrète au bout d'un certain temps.
La base est exactement la meme, il va juste falloir que le Math.cos tende vers 0.
Il y a plein de moyens de faire ça. En gros, on veut un truc comme ça :
Math.cos(time*cercle*freq)*amp*DEC
On veut donc que DEC aille de 1 à 0. Il y a différente façon de faire ça, le control va s'effectuer sur la façon dont on va de 1 à 0.
On peut par exemple créer un paramètre glissière qu'on va faire varier de 1 à 0, en jouant sur la courbe pour avoir l'effet voulu.
Je le montre meme pas, vous savez le faire ça.
Je vous montre un autre moyen, avec Math.exp. Cette fonction ici est assez légitime, car comme vous le savez, b=Math.exp(a), avec a qui évolue linéairement, b augmente en accélérant.
On peut par exemple vouloir que la décélération soit de plus en plus rapide. En d'autre terme, plus le haricot sera lent, plus il est freiné :
cercle=Math.PI*2;
freq=4;
amp=80;
dec=Math.max(2-Math.exp(time/2.5),0);
Math.cos(time*cercle*freq)*amp*dec
voyons la ligne rouge.
On veut donc que dec aille de 1 à 0. On veut qu'il reste quelques temps autour de 1, puis que ça chute vers 0 accélère.
Math.exp(time) augmente de en accélérant. Pour rappelle, Math.exp(0)=1
donc 1-Math.exp(time) demarre à 0, et diminue en accélérant.
On veut partir de 1, donc :
2-Math.exp(time) demarre à 1, et diminue en accélérant.
On veut s'arrêter à 0, donc :
Math.max( 2-Math.exp(time) , 0 ) une fois que 2-Math.exp(time) passe sous 0, on reste à 0.
J'ai divisé time par 2.5 pour ralentir le freinage. Cette valeur peut biensur être un paramètre glissière pour etre réglable à souhait.

et voilà !!!
un exemple, ou les vitesses de vibration et de freinage sont en fonction de la taille de la boule, comme dans la vraie vie bio.

voyons à présent une autre utilisation citée précédemment, l'oscillation.
Comme nous l'avons vu, quand une valeur évolue de manière linéaire, son cos et son sin oscillent entre -1 et 1. Je parle de valeur et non d'angle, car finalement, on se fiche qu'il s'agisse d'un angle ou pas. Un angle est une valeur, donc n'importe quelle valeur a son cos et son sin.
Alors voilà, nous voulons faire osciller un petit baton de droite à gauche, comme ceci :

On le comprend, la valeur de rotation ici correspond au cos (ou au sin) d'un angle qui évolue de manière linéaire. Nous allons donc créer la valeur d'un angle fictif :
cercle=Math.PI*2;
hop, on a crée un constante qui correspond au périmètre du cercle (c'est une bonne habitude pour etre précis dans ce qu'on fait) freq=2;
ça, ça va etre le nombre de tour à la seconde que fait notre angle.
amp=40;
ça, ça va etre l'amplitude non pas de cet angle, mais de celui que nous appliquerons au final au haricot bio.
Math.cos(time*cercle*freq)*amp
et ça, c'est la dernière phrase.
Dans le Math.cos, on a bien notre angle en radian qui évolue, qui effectue un tour de périmètre (cercle) tous les tours (time), multiplié par 2 (freq), le tout, multiplié par amp.
Attention !! amp multiplie bien l'ensemble du Math.cos, et non pas à l'interieur de la parenthèse. Souvenez vous, le cos et le sin n'évoluent que de -1 à 1. Avec le amp à 40, le haricot bio va de -40 à 40.
Maintenant, nous voulons que le haricot bio soit freiné par l'air, et s'arrète au bout d'un certain temps.
La base est exactement la meme, il va juste falloir que le Math.cos tende vers 0.
Il y a plein de moyens de faire ça. En gros, on veut un truc comme ça :
Math.cos(time*cercle*freq)*amp*DEC
On veut donc que DEC aille de 1 à 0. Il y a différente façon de faire ça, le control va s'effectuer sur la façon dont on va de 1 à 0.
On peut par exemple créer un paramètre glissière qu'on va faire varier de 1 à 0, en jouant sur la courbe pour avoir l'effet voulu.
Je le montre meme pas, vous savez le faire ça.
Je vous montre un autre moyen, avec Math.exp. Cette fonction ici est assez légitime, car comme vous le savez, b=Math.exp(a), avec a qui évolue linéairement, b augmente en accélérant.
On peut par exemple vouloir que la décélération soit de plus en plus rapide. En d'autre terme, plus le haricot sera lent, plus il est freiné :
cercle=Math.PI*2;
freq=4;
amp=80;
dec=Math.max(2-Math.exp(time/2.5),0);
Math.cos(time*cercle*freq)*amp*dec
voyons la ligne rouge.
On veut donc que dec aille de 1 à 0. On veut qu'il reste quelques temps autour de 1, puis que ça chute vers 0 accélère.
Math.exp(time) augmente de en accélérant. Pour rappelle, Math.exp(0)=1
donc 1-Math.exp(time) demarre à 0, et diminue en accélérant.
On veut partir de 1, donc :
2-Math.exp(time) demarre à 1, et diminue en accélérant.
On veut s'arrêter à 0, donc :
Math.max( 2-Math.exp(time) , 0 ) une fois que 2-Math.exp(time) passe sous 0, on reste à 0.
J'ai divisé time par 2.5 pour ralentir le freinage. Cette valeur peut biensur être un paramètre glissière pour etre réglable à souhait.

et voilà !!!
un exemple, ou les vitesses de vibration et de freinage sont en fonction de la taille de la boule, comme dans la vraie vie bio.

mardi 17 mars 2009
la trigolo
Aller on s'y met, on passe à la trigonométrie.
Derrière ce mot barbare se cache vos pires souvenirs du collège. Oui je dis bien collège et non lycée, car dans mes souvenirs, il s'agit du programme de 4eme, honte à vous donc.
Commençons par ce petit dessin :

Petite précision avant tout. Le dessin ci dessus est celui que vous verrez partout.
Toutefois, le point [0,0] de la composition d'AE est en haut à gauche. Ca veut dire que Y augmente de valeur en descendant. Donc inversé le 1 et le -1 de l'axe verticale dans votre tete quand vous etes dans aE.
Alors alors, kénécé...
Nous allons voir la trigonométrie uniquement dans la partie qui nous interesse, celle qui s'applique à After Effect.
La trigonométrie nous dit ceci :
-A chaque angle correspond un sinus, un cosinus et une tangente.
-le cosinus et le sinus sont compris entre -1 et 1
-cos(A)+sin(A)=1
Comme vous le voyez sur le dessin, à l'angle A correspond un cosinus environ égale à 0,4, un sinus environ égale à 0,9, et une tangente environ égale à 2.
Pour le moment nous allons nous intéresser au cosinus et au sinus.
Le cercle ayant un rayon de 1, on comprend pourquoi sin et cos varient de -1 à 1. Et en faisant augmenter l'angle à vitesse constante, vous comprenez ainsi que le cos et le sin vont osciller de -1 à 1. vous comprenez également instinctivement que lorsque l'angle A est proche de 90° (barre verte verticale) le sin s'attarde autour de 1, puis replonge brusquement vers 0 puis -1.
C'est pour cela qu'on parle par exemple de courbe sinusoïdale. L'allé-retour est arrondi aux extrémité, il en va exactement de même pour le cosinus.
Grace à ce dessin, vous comprenez également que le sin et le cos soient des vases communicants.
Quand sin=1, alors cos=0, et inversement.
Mais alors concrètement, dans after effect, à quoi ça va nous servir ?
Très concrètement, à trois choses :
-traduire un angle en position.
-traduire une position en angle.
-créer un phénomène oscillatoire.
Comment ça traduire un angle en positon ???
Et bien oui, regarder le dessin. On comprend que pour l'angle A correspond un point sur le cercle, de coordonnées [cos,sin]
Et inversement, si on a un point de coordonnée [x,y], on peut donc trouver son angle par rapport à un autre objet.
Passons à un peu de pratique, et voyons un point important.
Vous ètes habitués aux angles en degrés, de 0 à 360. C'est d'ailleurs la mesure utilisée par AE pour les rotations.
MAIS pour la trigonométrie, on utilise non pas les degrés, mais les radians.
Alors avant de dire beurk, voyons ce que c'est.
Comme vous savez, le périmètre d'un cercle se trouve par cette "formule" : Pi*R*2, ou R est le rayon.
Ici, notre cercle a un rayon de 1, donc son périmètre vaut 2*Pi.
Voilà comment fonctionnent les radians.
L'angle A vaut la section du périmètre du cercle délimité par l'angle.
On comprend donc que si A=90 en degré, on a donc un 1/4 de cercle, l'angle A vaut donc Pi/2 en radian.
180 degré=Pi
270 degré=(3*pi)/2
etc
Mais ne vous inquiétez pas, vous n'aurez pas à les calculer, AE a une fonction qui sert à ça.
L'important est de le savoir pour ne pas faire d'erreur, c'est un grand classique.
Ca veut dire que quand on écrit cos(A), A doit etre en radian.
Et comme souvent, A sera en dégré (car récupéré sur la valeur de rotation d'un calque), on écrira ça :
cos ( degreesToRadians ( A ) )
Et quand on voudra faire l'inverse, on utilisera RadiansToDegrees, on verra dans quel cas.
Un peu de pratique pour détendre tout le monde.
Créez un petit calque carré.
Dans sa postion, écrivez ceci :
vitesse=2*Math.PI*time;
diametre=50;
x=Math.cos(vitesse)*diametre;
y=Math.sin(vitesse)*diametre;
[x,y]+value
Et hop, un petit carré qui tourne autour d'un centre, mais sans rotation, il s'agit de sa position. D'ailleurs comme le voyez, il reste droit comme un i.
Explication :
vitesse=2*Math.PI*time; on définit la variable, selon le temps ici. comme 2*Pi vaut un tour complet, on comprend quand quand time=1, ça fait 1 tour, quand time=3, ça fait 3 tours.
diametre=50; Comme cos et sin varient de -1 à 1, on comprend qu'il faille augmenter la valeur, sinon notre carré va tourner autour du cercle de base, qui va de -1 à 1, c'est tout petit.
x=Math.cos(vitesse)*diametre;
y=Math.sin(vitesse)*diametre;
[x,y]+value
La suite est sans histoire. J'ai rajouté +value, car sinon, le carré tournerait autour du coin supérieur gauche de votre composition, puisqu'il évoluerait dans les 2 dimensions de -50 à 50.
le +value permet donc de le placer où l'on veut, ou même de l'animer.
Et là vous vous dites "hey cool, je peux aussi changer au cours le diamètre pour créer une spirale !!"
oui oui, vous pouvez, faites donc.

Derrière ce mot barbare se cache vos pires souvenirs du collège. Oui je dis bien collège et non lycée, car dans mes souvenirs, il s'agit du programme de 4eme, honte à vous donc.
Commençons par ce petit dessin :

Petite précision avant tout. Le dessin ci dessus est celui que vous verrez partout.
Toutefois, le point [0,0] de la composition d'AE est en haut à gauche. Ca veut dire que Y augmente de valeur en descendant. Donc inversé le 1 et le -1 de l'axe verticale dans votre tete quand vous etes dans aE.
Alors alors, kénécé...
Nous allons voir la trigonométrie uniquement dans la partie qui nous interesse, celle qui s'applique à After Effect.
La trigonométrie nous dit ceci :
-A chaque angle correspond un sinus, un cosinus et une tangente.
-le cosinus et le sinus sont compris entre -1 et 1
-cos(A)+sin(A)=1
Comme vous le voyez sur le dessin, à l'angle A correspond un cosinus environ égale à 0,4, un sinus environ égale à 0,9, et une tangente environ égale à 2.
Pour le moment nous allons nous intéresser au cosinus et au sinus.
Le cercle ayant un rayon de 1, on comprend pourquoi sin et cos varient de -1 à 1. Et en faisant augmenter l'angle à vitesse constante, vous comprenez ainsi que le cos et le sin vont osciller de -1 à 1. vous comprenez également instinctivement que lorsque l'angle A est proche de 90° (barre verte verticale) le sin s'attarde autour de 1, puis replonge brusquement vers 0 puis -1.
C'est pour cela qu'on parle par exemple de courbe sinusoïdale. L'allé-retour est arrondi aux extrémité, il en va exactement de même pour le cosinus.
Grace à ce dessin, vous comprenez également que le sin et le cos soient des vases communicants.
Quand sin=1, alors cos=0, et inversement.
Mais alors concrètement, dans after effect, à quoi ça va nous servir ?
Très concrètement, à trois choses :
-traduire un angle en position.
-traduire une position en angle.
-créer un phénomène oscillatoire.
Comment ça traduire un angle en positon ???
Et bien oui, regarder le dessin. On comprend que pour l'angle A correspond un point sur le cercle, de coordonnées [cos,sin]
Et inversement, si on a un point de coordonnée [x,y], on peut donc trouver son angle par rapport à un autre objet.
Passons à un peu de pratique, et voyons un point important.
Vous ètes habitués aux angles en degrés, de 0 à 360. C'est d'ailleurs la mesure utilisée par AE pour les rotations.
MAIS pour la trigonométrie, on utilise non pas les degrés, mais les radians.
Alors avant de dire beurk, voyons ce que c'est.
Comme vous savez, le périmètre d'un cercle se trouve par cette "formule" : Pi*R*2, ou R est le rayon.
Ici, notre cercle a un rayon de 1, donc son périmètre vaut 2*Pi.
Voilà comment fonctionnent les radians.
L'angle A vaut la section du périmètre du cercle délimité par l'angle.
On comprend donc que si A=90 en degré, on a donc un 1/4 de cercle, l'angle A vaut donc Pi/2 en radian.
180 degré=Pi
270 degré=(3*pi)/2
etc
Mais ne vous inquiétez pas, vous n'aurez pas à les calculer, AE a une fonction qui sert à ça.
L'important est de le savoir pour ne pas faire d'erreur, c'est un grand classique.
Ca veut dire que quand on écrit cos(A), A doit etre en radian.
Et comme souvent, A sera en dégré (car récupéré sur la valeur de rotation d'un calque), on écrira ça :
cos ( degreesToRadians ( A ) )
Et quand on voudra faire l'inverse, on utilisera RadiansToDegrees, on verra dans quel cas.
Un peu de pratique pour détendre tout le monde.
Créez un petit calque carré.
Dans sa postion, écrivez ceci :
vitesse=2*Math.PI*time;
diametre=50;
x=Math.cos(vitesse)*diametre;
y=Math.sin(vitesse)*diametre;
[x,y]+value
Et hop, un petit carré qui tourne autour d'un centre, mais sans rotation, il s'agit de sa position. D'ailleurs comme le voyez, il reste droit comme un i.
Explication :
vitesse=2*Math.PI*time; on définit la variable, selon le temps ici. comme 2*Pi vaut un tour complet, on comprend quand quand time=1, ça fait 1 tour, quand time=3, ça fait 3 tours.
diametre=50; Comme cos et sin varient de -1 à 1, on comprend qu'il faille augmenter la valeur, sinon notre carré va tourner autour du cercle de base, qui va de -1 à 1, c'est tout petit.
x=Math.cos(vitesse)*diametre;
y=Math.sin(vitesse)*diametre;
[x,y]+value
La suite est sans histoire. J'ai rajouté +value, car sinon, le carré tournerait autour du coin supérieur gauche de votre composition, puisqu'il évoluerait dans les 2 dimensions de -50 à 50.
le +value permet donc de le placer où l'on veut, ou même de l'animer.
Et là vous vous dites "hey cool, je peux aussi changer au cours le diamètre pour créer une spirale !!"
oui oui, vous pouvez, faites donc.

rubrique:
after effect expression trigonometrie
jeudi 5 février 2009
restons groupés et en ligne, merci. Et que ça soit joli aussi merci
Alors bon, oui je sais, j'ai promis le graal, le sésame, la trigonométrie, promis, bientôt.
Mais je fais un rapide détour par les vecteurs.
Souvenez vous, on a vu comment placer une image devant un spot pour que cette dernière soit projetée comme une vulgaire diapositive dont personne n'a plus besoin. On avait utiliser les vecteurs pour ça.
Voyons aujourd'hui une autre utilisation des vecteurs :
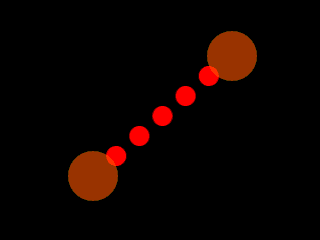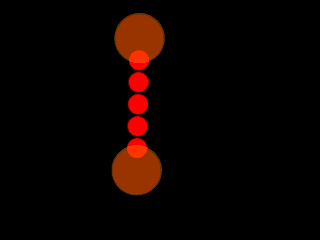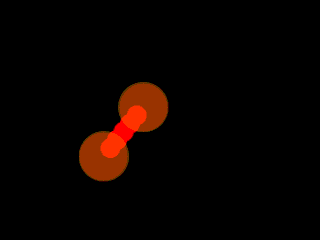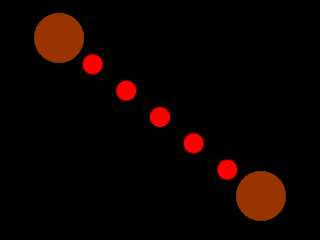
Comme vous l'aurez compris, comment faire pour que des calques soient entre deux calques, qu'ils y restent, qu'ils soient tous équidistants, et qu'ils s'adaptent selon leur nombre.
Ouais, tout ça...
C'est parti :
Commençons simple, créez deux solides oranges, ils seront les cibles. Mettez les légèrement en transparence, pour que l'on puisse voir en dessous, comme des coquins.
Créez un Null que vous allez appeler "plafond", et placez le sous les deux calques.
Créez un autre Null, nommez le "sol", et placez le tout en bas.
Nous allons voir l'utilité de ces deux calques.
Créez un petit calque rouge par exemple. Placez le entre plafond et sol.
Créez une expression pour sa position :
a=thisComp.layer("A").transform.position;
b=thisComp.layer("B").transform.position;
plafond=thisComp.layer("plafond").index;
nombre=thisComp.layer("sol").index-plafond-1;
c'est ultra simple : a et b sont les positions respectives des deux calques principaux, plafond est l'index du plafond, et nombre sera le nombre de calques placés entre plafond et sol.
En effet, s'il y a 5 calque entre plafond et sol, plafond aura 3 comme index, et sol aura 3+5+lui=9 comme index. donc 9-3-1=5, on a bien le nombre de calques.
J'ai crée les calques plafond et sol pour pouvoir avoir autant de calques que je veux dans la composition. Tant que mes calques rouges resteront entre plafond et sol, tout ira bien.
Voilà comment on va procéder.
Tous les calques partiront de a.
On va crée un vecteur V qui va de a vers b.
Donc si un calque par de a, et qu'on rajoute le vecteur, le calque sera sur b.
Si on fait a+V/2, le calque sera donc entre a et b, pile au milieu.
Donc, on va diviser la taille de V en autant de fois qu'il faut, donc en autant de calques présents.
écrivez à la suite :
V=sub(b,a);
donc ça, pas de problème, vous vous souvenez, on crée un vecteur qui va de a vers b.
I=index-plafond;
On utilise I comme nouvel index de calque, pour que ce dernier soit relatif à la position de "plafond" dans la composition.
increment=linear(I,0,nombre+1,0,1)
C'est ici que tout se joue.
La position du calque dépend de sa position dans la composition. Selon sa position, on va lui appliquer a+V*x, ou x varie donc de 0 à 1 (de 0% à 100% du vecteur donc)
La variable est donc la position dans la timeline, I.
Disons que N est le nombre de calques à placer.
I va donc varier de 1 à N, mais nous allons la faire varier de 0 à N+1, et nous allons voir pourquoi.
Donc, quand I=0, increment vaut 0. Et quand I vaut le nombre total de calques (le dernier calque de la liste donc), incrément vaut 1.
la dernière ligne :
a+V*increment
On rajoute donc V*increment à "a".
Donc quand increment vaut 1, on rajoute la valeur entière de V à a, on tombe donc sur b.
C'est pour cela que j'ai écrit increment=linear(I,0,nombre+1,0,1) et non increment=linear(I,1,nombre,0,1), car sinon, le premier calque aurait été à la meme position que le calque a, puisque on aurait eu a+V*0, et pareil pour dernier calque avec a+V*1.
Donc en écrivant increment=linear(I,0,nombre+1,0,1), les valeurs 0 et 1 pour incrément ne sont pas utilisées, puisque I ne peut varier que de 1 à nombre.
l'expression en entier :
a=thisComp.layer("A").transform.position;
b=thisComp.layer("B").transform.position;
plafond=thisComp.layer("plafond").index;
nombre=thisComp.layer("sol").index-plafond-1;
V=sub(b,a);
I=index-plafond;
increment=linear(I,0,nombre+1,0,1)
a+V*increment
une question que certains peuvent se poser:
on avait vu comment simplement placer un calque entre deux autres, c'était simple :
(a+b)/2
Alors pourquoi ne pas utiliser la meme technique en faisant varier "2" ?
Diviser par 3, on se rapproche de a, diviser par 1.5, on se rapproche de b.
Et bien car ça ne marche pas pour la situation suivante : quand b est à gauche de a.
Vous pouvez tester. En effet, si un calque a pour expression (a+b)/3, quand b passe à gauche de a, le calque ne restera pas collé à a, il ira vers b. Tout va s'inverser au moment de la bascule.
Et c'est bien normal, puisque quand on dit (a+b), on ne fait aucune différence entre les deux, alors que pour ce coup là, on en a besoin.
voilà, c'était simple non ?
Mais je fais un rapide détour par les vecteurs.
Souvenez vous, on a vu comment placer une image devant un spot pour que cette dernière soit projetée comme une vulgaire diapositive dont personne n'a plus besoin. On avait utiliser les vecteurs pour ça.
Voyons aujourd'hui une autre utilisation des vecteurs :

Comme vous l'aurez compris, comment faire pour que des calques soient entre deux calques, qu'ils y restent, qu'ils soient tous équidistants, et qu'ils s'adaptent selon leur nombre.
Ouais, tout ça...
C'est parti :
Commençons simple, créez deux solides oranges, ils seront les cibles. Mettez les légèrement en transparence, pour que l'on puisse voir en dessous, comme des coquins.
Créez un Null que vous allez appeler "plafond", et placez le sous les deux calques.
Créez un autre Null, nommez le "sol", et placez le tout en bas.
Nous allons voir l'utilité de ces deux calques.
Créez un petit calque rouge par exemple. Placez le entre plafond et sol.
Créez une expression pour sa position :
a=thisComp.layer("A").transform.position;
b=thisComp.layer("B").transform.position;
plafond=thisComp.layer("plafond").index;
nombre=thisComp.layer("sol").index-plafond-1;
c'est ultra simple : a et b sont les positions respectives des deux calques principaux, plafond est l'index du plafond, et nombre sera le nombre de calques placés entre plafond et sol.
En effet, s'il y a 5 calque entre plafond et sol, plafond aura 3 comme index, et sol aura 3+5+lui=9 comme index. donc 9-3-1=5, on a bien le nombre de calques.
J'ai crée les calques plafond et sol pour pouvoir avoir autant de calques que je veux dans la composition. Tant que mes calques rouges resteront entre plafond et sol, tout ira bien.
Voilà comment on va procéder.
Tous les calques partiront de a.
On va crée un vecteur V qui va de a vers b.
Donc si un calque par de a, et qu'on rajoute le vecteur, le calque sera sur b.
Si on fait a+V/2, le calque sera donc entre a et b, pile au milieu.
Donc, on va diviser la taille de V en autant de fois qu'il faut, donc en autant de calques présents.
écrivez à la suite :
V=sub(b,a);
donc ça, pas de problème, vous vous souvenez, on crée un vecteur qui va de a vers b.
I=index-plafond;
On utilise I comme nouvel index de calque, pour que ce dernier soit relatif à la position de "plafond" dans la composition.
increment=linear(I,0,nombre+1,0,1)
C'est ici que tout se joue.
La position du calque dépend de sa position dans la composition. Selon sa position, on va lui appliquer a+V*x, ou x varie donc de 0 à 1 (de 0% à 100% du vecteur donc)
La variable est donc la position dans la timeline, I.
Disons que N est le nombre de calques à placer.
I va donc varier de 1 à N, mais nous allons la faire varier de 0 à N+1, et nous allons voir pourquoi.
Donc, quand I=0, increment vaut 0. Et quand I vaut le nombre total de calques (le dernier calque de la liste donc), incrément vaut 1.
la dernière ligne :
a+V*increment
On rajoute donc V*increment à "a".
Donc quand increment vaut 1, on rajoute la valeur entière de V à a, on tombe donc sur b.
C'est pour cela que j'ai écrit increment=linear(I,0,nombre+1,0,1) et non increment=linear(I,1,nombre,0,1), car sinon, le premier calque aurait été à la meme position que le calque a, puisque on aurait eu a+V*0, et pareil pour dernier calque avec a+V*1.
Donc en écrivant increment=linear(I,0,nombre+1,0,1), les valeurs 0 et 1 pour incrément ne sont pas utilisées, puisque I ne peut varier que de 1 à nombre.
l'expression en entier :
a=thisComp.layer("A").transform.position;
b=thisComp.layer("B").transform.position;
plafond=thisComp.layer("plafond").index;
nombre=thisComp.layer("sol").index-plafond-1;
V=sub(b,a);
I=index-plafond;
increment=linear(I,0,nombre+1,0,1)
a+V*increment
une question que certains peuvent se poser:
on avait vu comment simplement placer un calque entre deux autres, c'était simple :
(a+b)/2
Alors pourquoi ne pas utiliser la meme technique en faisant varier "2" ?
Diviser par 3, on se rapproche de a, diviser par 1.5, on se rapproche de b.
Et bien car ça ne marche pas pour la situation suivante : quand b est à gauche de a.
Vous pouvez tester. En effet, si un calque a pour expression (a+b)/3, quand b passe à gauche de a, le calque ne restera pas collé à a, il ira vers b. Tout va s'inverser au moment de la bascule.
Et c'est bien normal, puisque quand on dit (a+b), on ne fait aucune différence entre les deux, alors que pour ce coup là, on en a besoin.
voilà, c'était simple non ?
Inscription à :
Articles (Atom)