Tout d'abord, reregardons ça:
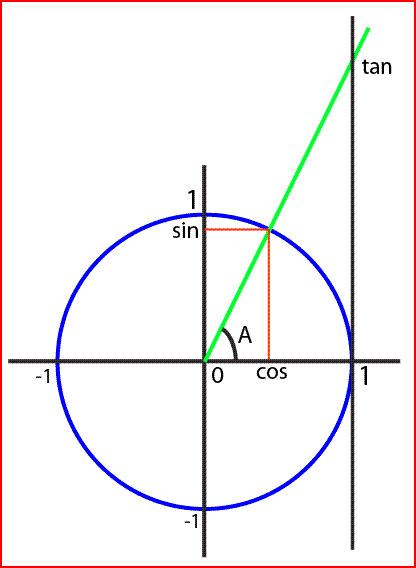
Imaginez que notre objet est sur le point 0, et que l'objet cible soit sur le point "tan", ou du moins sur l'axe de la ligne verte, ça revient au meme.
On cherche donc l'angle A.
Et bien on a cette formule :
tan(A)=coté opposé / coté adjacent.
Par coté adjacent, on parle du coté qui appartient à l'angle, est qui n'est pas la ligne verte (la ligne du cosinus donc, de 0 à 1)
Et par coté opposé, et bien c'est l'autre segment, celui qui n'appartient pas à l'angle (et toujours différent de la ligne verte), la ligne qui va donc de 1 à tan.
Passons à la pratique :
a=position;
b=thisComp.layer("Rouge sombre uni 1").transform.position;
Ca c'est simple, ce sont les deux variables de position. Celle du calque, et celle de la cible.
V=sub(b,a);
Là on crée le vecteur qui correspond à la ligne verte, la ligne qui va de a vers b.
radiansToDegrees ( Math.atan2 ( V[1],V[0] ))
Math.atan2 : il ne s'agit pas de la tangente, mais de la tangente dans le sens inverse.
Quand vous écrivez Math.tan(angle), ça vous donne la tangente de l'angle.
Math.atan2(tan), ça vous donne l'angle de la tangente.
Même chose pour avec Math.acos et Math.asin.
Petite finesse avec atan2, les deux "coté" sont séparés par une virgule.
Donc dans Math.atan2(), on doit inscrire la tangente, c'est donc coté opposé/coté adjacent.
C'est très simple, il suffit de prendre les composantes sur x et y du vecteur.
Reregardez le dessin, surtout la ligne verte. Le coté adjacent et le coté opposé corresponde bien aux composantes x et y de la ligne verte.
On note donc V[0] (sur x) et V[1] (sur y).
Et comme d'habitude, radiansToDegrees, car Math.atan2 donne un angle en radians.
Un petit exemple mixant plein de choses qu'on a vu, j'ai jamais dit que c'était joli.

On verra plus tard le coup de la taille qui change, mais vous avez les outils pour le faire.
